[注意]关于停止密码学讨论与试验的公开致歉信
发生何事？

车轮还要转，换个ID再来，学知识才重要

[原创]magma,/PARI/GP中文文档ECC初步:
SAGE:

几个数学家椭圆曲线的各种数据全包里了，

cremona，Stein-Watkins 的有理域，John Jones数域多项式

358K9s2c8@1M7q4)9K6b7g2)9J5c8W2)9J5c8Y4N6%4N6#2)9J5k6i4N6S2M7Y4N6A6j5$3E0Q4x3X3g2S2j5#2)9J5k6i4g2C8i4K6u0r3M7%4c8S2k6X3k6Q4x3V1k6v1i4K6u0W2c8g2)9J5k6f1y4J5k6h3#2G2L8X3q4Q4x3V1k6T1L8$3!0C8i4K6u0r3k6Y4g2D9L8s2c8W2P5s2c8Q4x3V1k6A6L8X3c8W2P5q4)9J5k6h3S2@1L8h3H3`.

前导子N分类的，默认前10000，可加载大的到130000

from sage.databases.cremona import LargeCremonaDatabase

随机选一条：
CremonaDatabase().random()

Elliptic Curve defined by y^2 + x*y = x^3 - x^2 + 324*x - 18068 over
Rational FieldElliptic Curve defined by y^2 + x*y = x^3 - x^2 + 324*x - 18068 over Rational Field

新老版cremona字母转换：
old_cremona_letter_code(5221)

'UUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUU\
UUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUU\
UUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUU'

标签分离：
c = CremonaDatabase()

parse_cremona_label('37a2')

import sage.databases.cremona as cremona

cremona.split_code('37a2')

求前导子21的所有曲线：
c = CremonaDatabase()

c.allcurves(21)

{'a1': [[1, 0, 0, -4, -1], 0, 8], 'a3': [[1, 0, 0, -39, 90], 0, 8],
'a2': [[1, 0, 0, -49, -136], 0, 4], 'a5': [[1, 0, 0, -784, -8515], 0,
2], 'a4': [[1, 0, 0, 1, 0], 0, 4], 'a6': [[1, 0, 0, -34, -217], 0, 2]}{'a1': [[1, 0, 0, -4, -1], 0, 8], 'a3': [[1, 0, 0, -39, 90], 0, 8], 'a2': [[1, 0, 0, -49, -136], 0, 4], 'a5': [[1, 0, 0, -784, -8515], 0, 2], 'a4': [[1, 0, 0, 1, 0], 0, 4], 'a6': [[1, 0, 0, -34, -217], 0, 2]}

从5个不变量定义曲线:要CremonaData理的才行：
c = CremonaDatabase()
sage: c.elliptic_curve_from_ainvs(11, [0, -1, 1, -10, -20])

列出给定前导子的所有曲线：
c = CremonaDatabase()

CremonaDatabase().list([3171])

[Elliptic Curve defined by y^2 + y = x^3 - x^2 - 7*x - 9 over Rational
Field, Elliptic Curve defined by y^2 + x*y + y = x^3 + x^2 - 49*x - 58
over Rational Field, Elliptic Curve defined by y^2 + x*y + y = x^3 + x^2
- 454*x + 3506 over Rational Field, Elliptic Curve defined by y^2 + x*y
+ y = x^3 + x^2 - 7249*x + 234536 over Rational Field, Elliptic Curve
defined by y^2 + x*y + y = x^3 + x^2 - 139*x + 8672 over Rational Field,
Elliptic Curve defined by y^2 + y = x^3 + x^2 - 14*x + 3677 over
Rational Field][Elliptic Curve defined by y^2 + y = x^3 - x^2 - 7*x - 9 over Rational Field, Elliptic Curve defined by y^2 + x*y + y = x^3 + x^2 - 49*x - 58 over Rational Field, Elliptic Curve defined by y^2 + x*y + y = x^3 + x^2 - 454*x + 3506 over Rational Field, Elliptic Curve defined by y^2 + x*y + y = x^3 + x^2 - 7249*x + 234536 over Rational Field, Elliptic Curve defined by y^2 + x*y + y = x^3 + x^2 - 139*x + 8672 over Rational Field, Elliptic Curve defined by y^2 + y = x^3 + x^2 - 14*x + 3677 over Rational Field]
列出给定前导子的所有曲线数：
c = CremonaDatabase()
c.number_of_curves(9920)
70
FSD猜想。千年问题：

c = CremonaDatabase()

c.allbsd(11)
{'a1': ['5', '1.2692093042795534217', '0.25384186085591068434', '1',
'1.00000000000000000000'], 'a3': ['1', '6.3460465213977671084',
'0.25384186085591068434', '1', '1'], 'a2': ['1',
'0.25384186085591068434', '0.25384186085591068434', '1',
'1.00000000000000000000']}{'a1': ['5', '1.2692093042795534217', '0.25384186085591068434', '1', '1.00000000000000000000'], 'a3': ['1', '6.3460465213977671084', '0.25384186085591068434', '1', '1'], 'a2': ['1', '0.25384186085591068434', '0.25384186085591068434', '1', '1.00000000000000000000']}

SAGE连千年问题黎曼零点都整合了，10万个，精度10^9，图灵，冯诺曼依都算过黎曼零点，《美丽心灵》纳什就是想解决黎曼零点问题发疯的

zz = zeta_zeros()
zz
zz[100] --------第一百个

[14.134725142000001, 21.022039638999999, 25.01085758,
30.424876126000001, 32.935061588000003, 37.586178158999999,
40.918719011999997, 43.327073280999997, 48.005150880999999,
49.773832478000003, 52.970321478000002, 56.446247696999997,
59.347044003000001, 60.831778524999997, 65.112544048000004,
67.079810529, 69.546401711000001, 72.067157674000001,
75.704690698999997, 77.144840068999997, 79.337375019999996,
82.910380853999996, 84.735492980999993, 87.425274612999999,
88.809111208000004, 92.491899270999994, 94.651344041000002,
95.870634228, 98.831194217999993,

SAGE把在线整数列也包了

de1K9s2c8@1M7q4)9K6b7g2)9J5c8W2)9J5c8X3!0W2K9i4y4Q4x3X3g2G2M7X3N6Q4x3V1j5`.

按编号找数列：
SloaneEncyclopedia[6083]

[1, 2, 1, 3, 1, 1, 1, 3, 3, 3, 1, 3, 1, 3, 5, 3, 1, 5, 1, 3, 7, 3, 1, 7,
1, 3, 9, 3, 1, 9, 1, 3, 11, 3, 1, 11, 1, 3, 13, 3, 1, 13, 1, 3, 15, 3,
1, 15, 1, 3, 17, 3, 1, 17, 1, 3, 19, 3, 1, 19, 1, 3, 21, 3, 1, 21, 1, 3,
23, 3, 1, 23, 1, 3, 25, 3, 1, 25, 1, 3, 27, 3, 1, 27, 1, 3, 29, 3, 1,
29, 1, 3, 31, 3][1, 2, 1, 3, 1, 1, 1, 3, 3, 3, 1, 3, 1, 3, 5, 3, 1, 5, 1, 3, 7, 3, 1, 7, 1, 3, 9, 3, 1, 9, 1, 3, 11, 3, 1, 11, 1, 3, 13, 3, 1, 13, 1, 3, 15, 3, 1, 15, 1, 3, 17, 3, 1, 17, 1, 3, 19, 3, 1, 19, 1, 3, 21, 3, 1, 21, 1, 3, 23, 3, 1, 23, 1, 3, 25, 3, 1, 25, 1, 3, 27, 3, 1, 27, 1, 3, 29, 3, 1, 29, 1, 3, 31, 3]

按数列找：
SloaneEncyclopedia.find([1,2,3,5,8], 1)  

Searching Sloane's online database...
[[45,
  'Fibonacci numbers: F(n) = F(n-1) + F(n-2), F(0) = 0, F(1) = 1, F(2) = 1, ...',
  [0,
   1,
   1,
   2,
   3,
   5,

按编号找名称：

sequence_name(12)

SAGE：
康威多项式。。。。。还活着就命名多项式了。。。。

c = ConwayPolynomials()
c.polynomial(3, 21)

约翰·何顿·康威，26个散单群里有板有3个他找的

1fdK9s2c8@1M7q4)9K6b7g2)9J5c8W2)9J5c8Y4N6%4N6#2)9J5k6h3S2#2k6r3!0F1k6#2)9J5k6h3y4G2L8g2)9J5c8Y4N6A6K9$3W2Q4x3V1k6Q4x3U0g2q4y4#2)9J5y4f1u0m8i4K6t1#2b7e0k6Q4x3U0g2q4y4#2)9J5y4f1u0r3i4K6t1#2b7U0m8Q4x3U0g2o6x3W2)9J5y4f1t1%4i4K6t1#2c8e0c8Q4x3U0g2n7c8q4)9J5y4e0V1#2i4K6t1#2c8e0W2Q4x3U0g2m8x3g2)9J5y4f1u0r3i4K6t1#2b7K6u0Q4x3U0g2n7y4#2)9J5y4f1f1#2i4K6t1#2b7V1q4Q4x3U0g2n7y4#2)9J5y4f1f1#2i4K6t1#2b7e0S2Q4x3U0f1^5x3b7`.`.

[求助]MORDELL定理问题
E00:=EllipticCurve( x^3-4*x^2+16);
E00;
MordellWeilShaInformation(E00);
DescentInformation(E00);
Generators(E00) ;
Q00, reps := IntegralPoints(E00);
Q00;
TorsionSubgroup(E00);

Elliptic Curve defined by y^2 = x^3 - 4*x^2 + 16 over Rational Field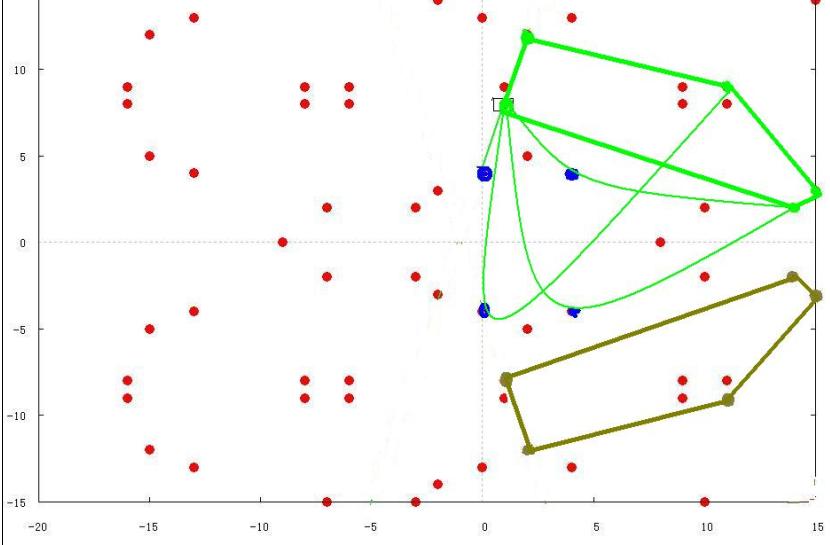


mod17
0
0 0
Torsion Subgroup = Z/5
Analytic rank = 0
     ==> Rank(E) = 0
[ 0, 0 ]
[]
[]
Torsion Subgroup = Z/5
Analytic rank = 0
     ==> Rank(E) = 0
[ 0, 0 ]
[]
[]
[ (0 : 4 : 1) ]
[ (0 : 4 : 1), (4 : -4 : 1) ]
Abelian Group isomorphic to Z/5
Defined on 1 generator
Relations:
    5*$.1 = 0

====================
Qx<x> := PolynomialRing(Rationals());
E0:=EllipticCurve( x^3-2*x+16);
E0;
MordellWeilShaInformation(E0);

DescentInformation(E0);
Generators(E0) ;
Q0, reps := IntegralPoints(E0);
Q0;
TorsionSubgroup(E0);

Elliptic Curve defined by y^2 = x^3 - 2*x + 16 over Rational Field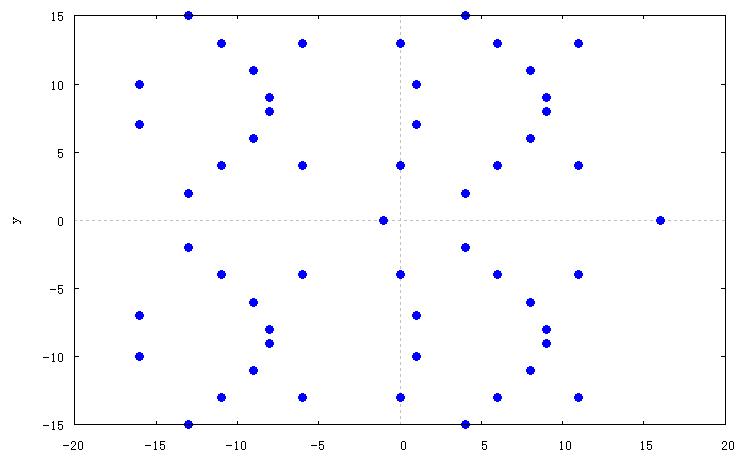



mod17
1
1 1
Torsion Subgroup is trivial
Analytic rank = 1
     ==> Rank(E) = 1
The 2-Selmer group has rank 1
Found a point of infinite order.
After 2-descent:
    1 <= Rank(E) <= 1
    Sha(E)[2] is trivial
(Searched up to height 100 on the 2-coverings.)
[ 1, 1 ]
[ (0 : 4 : 1) ]
[
    <2, [ 0, 0 ]>
]
Torsion Subgroup is trivial
Analytic rank = 1
     ==> Rank(E) = 1
The 2-Selmer group has rank 1
Found a point of infinite order.
After 2-descent:
    1 <= Rank(E) <= 1
    Sha(E)[2] is trivial
(Searched up to height 100 on the 2-coverings.)
[ 1, 1 ]
[ (0 : 4 : 1) ]
[
    <2, [ 0, 0 ]>
]
[ (0 : 4 : 1) ]
[ (0 : 4 : 1) ]
Abelian Group of order 1

===========================================

Qx<x> := PolynomialRing(Rationals());
E0:=EllipticCurve( x^3-x+16);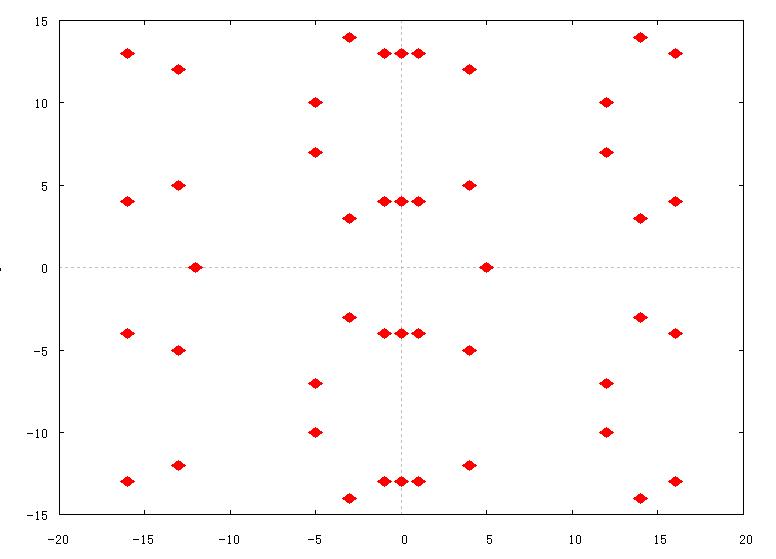

mod17



mod21
E0;
MordellWeilShaInformation(E0);

DescentInformation(E0);
Generators(E0) ;
Q0, reps := IntegralPoints(E0);
Q0;
TorsionSubgroup(E0);

Elliptic Curve defined by y^2 = x^3 - x + 16 over Rational Field
2
2 2
Torsion Subgroup is trivial
Analytic rank = 2
The 2-Selmer group has rank 2
Found a point of infinite order.
Found 2 independent points.
After 2-descent:
    2 <= Rank(E) <= 2
    Sha(E)[2] is trivial
(Searched up to height 100 on the 2-coverings.)
[ 2, 2 ]
[ (0 : 4 : 1), (1 : -4 : 1) ]
[
    <2, [ 0, 0 ]>
]

Torsion Subgroup is trivial
Analytic rank = 2
The 2-Selmer group has rank 2
Found a point of infinite order.
Found 2 independent points.
After 2-descent:
    2 <= Rank(E) <= 2
    Sha(E)[2] is trivial
(Searched up to height 100 on the 2-coverings.)
[ 2, 2 ]
[ (0 : 4 : 1), (1 : -4 : 1) ]
[
    <2, [ 0, 0 ]>
]
[ (1 : 4 : 1), (-1 : 4 : 1) ]
[ (-1 : -4 : 1), (0 : 4 : 1), (1 : -4 : 1), (16 : -64 : 1), (63 : 500 : 1), (65
: -524 : 1), (262016 : 134119436 : 1) ]
Abelian Group of order 1

[推荐]户照里的密码知识扫盲
4个，传了3。。。另一个自各下吧

[翻译]探索PE文件内幕—— Win32可移植可执行文件格式之旅
收藏，谢谢楼主

[转帖]逆向工程已成世界专利战的秘密武器
反对专利!反对专利!

[求助]MORDELL定理问题
Qx<x> := PolynomialRing(Rationals());
E1:=EllipticCurve( x^3-39);
E1;
MordellWeilRank(E1);
RankBounds(E1);
MordellWeilShaInformation(E1);
F:=FaltingsHeight(E1) ;
F;
HasComplexMultiplication(E1);
DescentInformation(E1);
Generators(E1) ;
Q1, reps := IntegralPoints(E1);
Q1;
TorsionSubgroup(E1);

Elliptic Curve defined by y^2 = x^3 - 39 over Rational Field
2
2 2
Torsion Subgroup is trivial
Analytic rank = 2
The 2-Selmer group has rank 2
Found a point of infinite order.
Found 2 independent points.
After 2-descent:
    2 <= Rank(E) <= 2
    Sha(E)[2] is trivial
(Searched up to height 100 on the 2-coverings.)
[ 2, 2 ]
[ (22 : -103 : 1), (4 : 5 : 1) ]
[
    <2, [ 0, 0 ]>
]
-0.204821688386087651093858399724
true -3
Torsion Subgroup is trivial
Analytic rank = 2
The 2-Selmer group has rank 2
Found a point of infinite order.
Found 2 independent points.
After 2-descent:
    2 <= Rank(E) <= 2
    Sha(E)[2] is trivial
(Searched up to height 100 on the 2-coverings.)
[ 2, 2 ]
[ (22 : -103 : 1), (4 : 5 : 1) ]
[
    <2, [ 0, 0 ]>
]
[ (4 : 5 : 1), (10 : 31 : 1) ]
[ (4 : 5 : 1), (10 : 31 : 1), (22 : -103 : 1) ]
Abelian Group of order 1

[求助]MORDELL定理问题
多谢！

先贴点慢慢理解

Qx<x> := PolynomialRing(Rationals());
E1:=EllipticCurve( x^3-39);-

E1;
jInvariant(E1);
Genus(E1);

Q1, reps := IntegralPoints(E1);
Q1;
TorsionSubgroup(E1);-------------------------------------RANK=2，T=1
Mordell's curve   E: y^2 = x^3 - 39                       %%%
%%%                                                                       %%%
%%%    E_-00039: r = 2   t = 1   #III =  1                                %%%
%%%              E(Q) = <(4, 5)> x <(10, 31)>                             %%%
%%%              R =   2.7347941297                                       %%%
%%%               6 integral points                                       %%%
%%%                1. (4, 5) = 1 * (4, 5)                                 %%%
%%%                2. (4, -5) = -(4, 5)                                   %%%
%%%                3. (22, 103) = 1 * (4, 5) - 1 * (10, 31)               %%%
%%%                4. (22, -103) = -(22, 103)                             %%%
%%%                5. (10, 31) = 1 * (10, 31)                             %%%
%%%                6. (10, -31) = -(10, 31)   

Elliptic Curve defined by y^2 = x^3 - 39 over Rational Field
0
1
[ (4 : 5 : 1), (10 : 31 : 1), (22 : -103 : 1) ]
Abelian Group of order 1
==========================

E2:=EllipticCurve(x^3 +1331);---------------------------------RANK=1，T=2
E2;
jInvariant(E2);
Genus(E2);
TorsionSubgroup(E2);
Q2, reps := IntegralPoints(E2);
Q2;
E_+01331: r = 1   t = 2   #III =  1
          E(Q) = <(37, 228)> x <(-11, 0)>
          R =   3.2472475292
           3 integral points
            1. (-11, 0) = (-11, 0)
            2. (37, 228) = 1 * (37, 228)
            3. (37, -228) = -(37, 228)
Elliptic Curve defined by y^2 = x^3 + 1331 over Rational Field
0
1
Abelian Group isomorphic to Z/2
Defined on 1 generator
Relations:
    2*$.1 = 0
[ (-11 : 0 : 1), (37 : -228 : 1) ]
=========================

E3:=EllipticCurve(x^3 - 9998);------RANK=3，T=1 无整点
E3;
jInvariant(E3);
Genus(E3);
TorsionSubgroup(E3);
Q3, reps := IntegralPoints(E3);
Q3;

r = 3   t = 1   #III =  1
          E(Q) = <(-71/4, 531/8)> x <(19/9, 2701/27)> x <(283/9, 5473/27)>
          R = 114.5499715889
           0 integral points
Elliptic Curve defined by y^2 = x^3 - 9998 over Rational Field
0
1
Abelian Group of order 1
[]

==========================
E6:=EllipticCurve(x^3 +1521);----------RANK=1，T=3，有三对整点
E6;
jInvariant(E6);
Genus(E6);
TorsionSubgroup(E6);
Q6, reps := IntegralPoints(E6);
Q6;
E_+01521: r = 1   t = 3   #III =  1
          E(Q) = <(12, 57)> x <(0, 39)>
          R =   1.9164245639
           6 integral points
            1. (0, 39) = (0, 39)
            2. (0, -39) = -(0, 39)
            3. (12, 57) = 1 * (12, 57)
            4. (12, -57) = -(12, 57)
            5. (52, 377) = (0, 39) - 1 * (12, 57)
            6. (52, -377) = -(52, 377)
Elliptic Curve defined by y^2 = x^3 + 1521 over Rational Field
0
1
Abelian Group isomorphic to Z/3
Defined on 1 generator
Relations:
    3*$.1 = 0
[ (0 : 39 : 1), (12 : -57 : 1), (52 : 377 : 1) ]

E5:=EllipticCurve(x^3 -4*x^2+16);-----RANK=？，T=1，整点？
E5;
jInvariant(E5);
Genus(E5);
TorsionSubgroup(E5);
Q5, reps := IntegralPoints(E5);
Q5;

E7:=EllipticCurve(x^3 + 7388);
E7;
jInvariant(E7);
Genus(E7);
TorsionSubgroup(E7);
Q7, reps := IntegralPoints(E7);
Q7;

E8:=EllipticCurve(x^3 +7428);
E8;

jInvariant(E8);
Genus(E8);
TorsionSubgroup(E8);
Q8, reps := IntegralPoints(E8);
Q8;

E9:=EllipticCurve(x^3 - 7416);
E9;
jInvariant(E9);
Genus(E9);
TorsionSubgroup(E9);
Q9, reps := IntegralPoints(E9);
Q9;

[转帖]硬件安全防范
GOOGLE.COM，有书名。但没内容。。。。

不要为难兄弟。。。

[分享]亿群大康，挑一个试试啊
492K9s2c8@1M7q4)9K6b7g2)9J5c8W2)9J5c8Y4N6%4N6#2)9J5k6h3g2I4N6h3&6Q4x3X3g2U0L8$3#2Q4x3V1k6X3L8%4u0#2L8g2)9J5c8Y4c8Z5M7X3g2S2k6q4)9J5k6o6p5%4x3o6p5I4i4K6u0V1x3g2)9J5k6o6q4Q4x3X3g2Z5N6r3#2D9

非主流数学、密码类项目 - 文章索引
原帖为其他非主流数学、密码类项目 - 文章索引
本帖对原帖有所增删修改。
版权归中国分布式计算总站所有。

BinSYS-SZDG —— 搜索高阶广义二进制数系
官方站点：d89K9s2c8@1M7q4)9K6b7g2)9J5c8W2)9J5c8Y4y4*7k6r3N6Q4x3X3g2D9M7r3c8K6i4K6u0W2M7%4A6@1j5h3E0A6i4K6u0W2K9s2g2Q4x3V1k6K6P5X3c8Y4i4K6u0r3
中文站点：59cK9s2c8@1M7q4)9K6b7g2)9J5c8W2)9J5c8X3u0G2K9h3&6U0i4K6u0W2k6i4q4#2L8W2)9J5k6h3y4G2L8g2)9J5c8Y4y4*7k6r3N6Q4x3V1k6V1k6i4y4U0i4K6g2X3L8Y4g2E0M7%4W2K6i4K6g2X3k6i4y4Q4x3X3g2Z5N6r3@1`.
项目介绍：SZDG 中的数学
项目指南：
项目新闻：5deK9s2c8@1M7q4)9K6b7g2)9J5c8W2)9J5c8Y4N6%4N6#2)9J5k6h3g2I4N6h3&6Q4x3X3g2U0L8$3#2Q4x3V1k6X3L8%4u0#2L8g2)9J5c8Y4k6A6k6i4N6@1K9l9`.`. ... =page%3D1#pid207584
相关帖子：SZDG、数系与其他、成功完成对11阶二进制数系的搜索

Enigma-M4-Project —— 破解四转子之谜
官方站点：5e6K9s2c8@1M7q4)9K6b7g2)9J5c8W2)9J5c8Y4N6%4N6#2)9J5k6h3u0&6N6r3g2J5k6h3g2X3i4K6u0W2L8%4u0Y4i4K6u0r3
中文站点：663K9s2c8@1M7q4)9K6b7g2)9J5c8W2)9J5c8Y4N6%4N6#2)9J5k6h3g2I4N6h3&6Q4x3X3g2U0L8$3#2Q4x3V1k6E0y4q4)9J5c8R3`.`.
项目介绍：家用电脑破译“二战”纳粹密码，破译者都是业余的、分布式计算破解 Enigma 代码
项目指南：Enigma项目(M4-Project)参加说明
相关帖子：

Enigma@home —— 破解四转子之谜（BOINC 平台）
官方站点：37dK9s2c8@1M7q4)9K6b7g2)9J5c8W2)9J5c8Y4N6%4N6#2)9J5k6h3g2F1K9h3N6E0j5h3q4@1K9r3!0E0k6g2)9J5k6h3&6W2N6q4)9J5c8R3`.`.
项目介绍：见“Enigma-M4-Project —— 破解四转子之谜”
相关帖子：[新项目]Enigma@Home

The 3x + 1 class record search —— 3x+1 问题
官方站点：5aeK9s2c8@1M7q4)9K6b7g2)9J5c8W2)9J5c8Y4N6%4N6#2)9J5k6h3g2J5K9h3y4J5i4K6u0W2L8X3I4Q4x3V1k6%4L8$3&6V1M7X3!0#2M7#2)9J5c8X3W2F1k6r3g2^5i4K6u0W2K9s2c8E0L8l9`.`.
中文站点：b4dK9s2c8@1M7q4)9K6b7g2)9J5c8W2)9J5c8Y4N6%4N6#2)9J5k6h3g2I4N6h3&6Q4x3X3g2U0L8$3#2Q4x3V1j5K6P5q4)9J5b7U0q4Q4x3V1j5`.
项目介绍：7faK9s2c8@1M7q4)9K6b7g2)9J5c8W2)9J5c8Y4N6%4N6#2)9J5k6h3g2I4N6h3&6Q4x3X3g2U0L8$3#2Q4x3V1k6V1K9i4y4@1M7X3W2T1N6i4c8W2k6q4)9J5c8X3q4H3i4K6u0V1L8h3q4@1K9q4)9J5k6h3S2@1L8h3I4Q4x3U0x3K6P5s2m8D9N6i4x3I4
项目指南：3x+1问题
相关帖子：3x+1Problem参加全攻略

PrimeGrid —— 质数网格
官方站点：bacK9s2c8@1M7q4)9K6b7g2)9J5c8W2)9J5c8Y4N6%4N6#2)9J5k6i4m8J5K9h3#2W2k6%4u0A6k6q4)9J5k6h3y4G2L8b7`.`.
项目介绍：673K9s2c8@1M7q4)9K6b7g2)9J5c8W2)9J5c8Y4N6%4N6#2)9J5k6h3g2I4N6h3&6Q4x3X3g2U0L8$3#2Q4x3V1k6V1K9i4y4@1M7X3W2T1N6i4c8W2k6q4)9J5c8X3q4H3i4K6u0V1j5%4u0&6M7s2c8G2i4K6u0W2K9s2c8E0L8q4)9J5x3%4m8J5K9h3#2W2k6%4u0A6k6l9`.`.
项目指南：00eK9s2c8@1M7q4)9K6b7g2)9J5c8W2)9J5c8Y4N6%4N6#2)9J5k6h3g2I4N6h3&6Q4x3X3g2U0L8$3#2Q4x3V1k6X3L8%4u0#2L8g2)9J5c8Y4k6A6k6i4N6@1K9s2u0W2j5h3c8Q4x3X3g2H3K9s2m8Q4x3@1k6@1K9h3c8Q4x3@1b7^5y4e0x3@1
项目新闻：f65K9s2c8@1M7q4)9K6b7g2)9J5c8W2)9J5c8Y4N6%4N6#2)9J5k6h3g2I4N6h3&6Q4x3X3g2U0L8$3#2Q4x3V1k6X3L8%4u0#2L8g2)9J5c8Y4k6A6k6i4N6@1K9s2u0W2j5h3c8Q4x3X3g2H3K9s2m8Q4x3@1k6@1K9h3c8Q4x3@1b7I4y4o6j5^5z5q4)9J5y4Y4m8A6k6q4)9K6c8o6t1H3y4K6f1%4x3W2)9J5y4Y4m8S2k6$3g2Q4x3@1b7I4i4K6t1$3k6i4S2@1M7X3q4Q4x3@1c8H3j5h3N6W2i4K6t1#2x3@1b7I4i4K6t1K6M7r3W2V1x3U0l9%4y4e0M7J5
相关帖子：[PrimeGrid 相关新闻] RSA-640 被分解、PrimeGrid FAQ 中英文对照、RieselSieve & PrimeGrid这两个项目有什么关系吗?、PrimeGrid子项目比较

RieselSieve —— Riesel 质数搜索
官方站点（传统）：5fbK9s2c8@1M7q4)9K6b7g2)9J5c8W2)9J5c8Y4N6%4N6#2)9J5k6i4u0A6k6i4y4W2L8s2y4A6k6i4k6W2i4K6u0W2j5$3!0E0
官方站点（BOINC）：640K9s2c8@1M7q4)9K6b7g2)9J5c8W2)9J5c8X3u0G2K9h3&6U0i4K6u0W2M7X3W2W2M7$3g2D9M7$3W2W2N6X3g2Q4x3X3g2U0L8$3@1`.
项目介绍：b45K9s2c8@1M7q4)9K6b7g2)9J5c8W2)9J5c8Y4N6%4N6#2)9J5k6h3g2I4N6h3&6Q4x3X3g2U0L8$3#2Q4x3V1k6V1K9i4y4@1M7X3W2T1N6i4c8W2k6q4)9J5c8X3q4H3i4K6u0V1L8h3q4@1K9q4)9J5k6h3S2@1L8h3I4Q4x3U0y4J5K9h3g2K6k6h3I4K6K9h3g2$3k6b7`.`.
项目新闻（BOINC）：bd9K9s2c8@1M7q4)9K6b7g2)9J5c8W2)9J5c8Y4N6%4N6#2)9J5k6h3g2I4N6h3&6Q4x3X3g2U0L8$3#2Q4x3V1k6X3L8%4u0#2L8g2)9J5c8Y4k6A6k6i4N6@1K9l9`.`. ... =page%3D1#pid207573
相关帖子：RieselSieve加入BOINC平台、RieselSieve & PrimeGrid这两个项目有什么关系吗?

Rectilinear Crossing Number —— 寻找平面化完全图最小交叉数
官方站点：8c9K9s2c8@1M7q4)9K6b7g2)9J5c8W2)9J5c8X3c8A6M7%4c8Q4x3X3g2A6M7%4c8Q4x3X3g2@1N6h3N6J5j5i4A6Q4x3X3g2S2N6q4)9J5c8X3y4S2M7r3f1#2i4K6u0r3
项目新闻：4abK9s2c8@1M7q4)9K6b7g2)9J5c8W2)9J5c8Y4N6%4N6#2)9J5k6h3g2I4N6h3&6Q4x3X3g2U0L8$3#2Q4x3V1k6X3L8%4u0#2L8g2)9J5c8Y4k6A6k6i4N6@1K9s2u0W2j5h3c8Q4x3X3g2H3K9s2m8Q4x3@1k6@1K9h3c8Q4x3@1b7I4y4o6j5^5z5q4)9J5y4Y4m8A6k6q4)9K6c8o6t1H3y4K6f1^5y4q4)9J5y4Y4m8S2k6$3g2Q4x3@1b7I4i4K6t1$3k6i4S2@1M7X3q4Q4x3@1c8H3j5h3N6W2i4K6t1#2x3@1b7I4i4K6t1K6M7r3W2V1x3U0p5&6y4o6j5^5
相关帖子：[新项目][数学类]Rectilinear Crossing Number

Sudoku —— 寻找最小唯一解数独
官方站点：ae3K9s2c8@1M7q4)9K6b7g2)9J5c8W2)9J5c8X3c8A6M7%4b7J5i4K6u0W2K9i4y4@1i4K6u0W2N6s2g2Y4M7X3q4*7i4K6u0W2j5i4c8Q4x3V1k6K6N6h3c8G2K9%4g2Q4x3V1j5`.
项目新闻：7a4K9s2c8@1M7q4)9K6b7g2)9J5c8W2)9J5c8Y4N6%4N6#2)9J5k6h3g2I4N6h3&6Q4x3X3g2U0L8$3#2Q4x3V1k6X3L8%4u0#2L8g2)9J5c8Y4k6A6k6i4N6@1K9s2u0W2j5h3c8Q4x3X3g2H3K9s2m8Q4x3@1k6@1K9h3c8Q4x3@1b7I4y4o6j5^5z5q4)9J5y4Y4m8A6k6q4)9K6c8o6t1J5y4e0f1K6y4g2)9J5y4Y4m8S2k6$3g2Q4x3@1b7I4i4K6t1$3k6i4S2@1M7X3q4Q4x3@1c8H3j5h3N6W2i4K6t1#2x3@1b7I4i4K6t1K6M7r3W2V1x3U0t1#2y4e0x3#2
相关帖子：[新项目][数学类]SUDOKU

NQueens Project —— 枚举 N 皇后问题的解
官方站点：0dfK9s2c8@1M7q4)9K6b7g2)9J5c8W2)9J5c8X3&6I4N6h3g2W2L8Y4y4Q4x3X3g2A6L8X3N6Q4x3X3g2#2k6r3g2U0i4K6u0W2j5$3I4Q4x3V1j5`.
相关帖子：[新项目] [算法类] NQueens Project

SHA-1 Collision Search Graz —— 寻找SHA-1算法的碰撞
官方站点：abeK9s2c8@1M7q4)9K6b7g2)9J5c8W2)9J5c8X3u0G2K9h3&6U0i4K6u0W2K9h3q4A6K9#2)9J5k6i4c8#2k6%4u0S2P5W2)9J5k6h3q4@1i4K6u0r3M7$3S2S2x3g2)9#2k6X3y4G2L8r3I4Q4y4h3k6K6k6h3q4J5j5$3S2Q4x3V1j5`.
相关帖子：SHA-1 Collision Search Graz - 寻找SHA-1算法的碰撞 - 新手指南

[求助]MORDELL定理问题
没人啊。。。刷墙涂鸦

[原创]magma,/PARI/GP中文文档ECC初步:
超椭圆曲线：

有理域下定义超椭圆曲线：
P<x> := PolynomialRing(RationalField());
> C := HyperellipticCurve(x^6+x^2+1);
C;
复域下定义超椭圆曲线：

P<x> := PolynomialRing(ComplexField());
> C := HyperellipticCurve(x^6+x^2+10);
C;
Hyperelliptic Curve defined by y^2 = x^6 + x^2 + 10.0000000000000000000000000000
over Complex field of precision 30

有限狱模17:
P1<x> := PolynomialRing(GF(17));
C17 := HyperellipticCurve(x^6+x^2+1);
C17;

P2<x> := PolynomialRing(GF(17));
C1717 := HyperellipticCurve(x^16+x^5+x^2+1);
C1717;

扭曲线:
Twists(C17);

同构吗?:
IsIsomorphic(C17, C1717);

tws,auts := Twists(C17);
tws;

是椭圆曲线吗?
IsEllipticCurve(C)

亏格数:
Genus(C);
Genus(C17);
Genus(C1717);
阶:
Degree(C);
Degree(C17);
Degree(C1717);

判别式:
Discriminant(C);

Discriminant(C17);
Discriminant(C1717);

P3<x> := PolynomialRing(GF(17));

> C2 := HyperellipticCurve(x^6+x^2+x+1);

J不变量:
JInvariants(C2);

绝对不变量:

AbsoluteInvariants(C2);

无限远点座标:
PointsAtInfinity(C);

PointsAtInfinity(C2);
PointsAtInfinity(C17);
求点:
Points(C : Bound := 1);
Points(C17 : Bound := 1);

Points(C2: Bound := 1);

自同构:
Aut(C);
Aut(C2);
Aut(C17) ;

Iso(C17, C2);

变为雅格布式
J1:=Jacobian(C);
J1;
J2:=Jacobian(C2);
J2;
J17:=Jacobian(C17);
J17;
变为雅格布式后求阶
Order(J2);
Order(J17);
Curve(C17)

外尔下降算法分解:

PP<x>:=PolynomialRing(GF(2));
> h := PP!1;
> f := x^7 + x^4 + x^3 + 1;
> J := Jacobian(HyperellipticCurve(f,h));  // a supersingular curve
> Jext := BaseExtend(J, 41);
> Factorization(#Jext);

> m := 177722253954175633;                 // some big subgroup order
> cofact := 3887047*7;
> P := cofact*Random(Jext);
> Q := 876213876263897634*P;               // Q in <P>

[推荐]推荐PARI和SAGE和MXGMA
NFS筛法分解，80位的要64 M of RAM ， 0.5 G of disk space

有个e7bK9s2c8@1M7q4)9K6b7g2)9J5c8W2)9J5c8Y4N6%4N6#2)9J5k6h3c8A6M7%4c8J5K9h3u0#2N6r3g2V1i4K6u0W2L8X3g2@1i4K6u0r3c8r3!0%4L8X3I4G2j5h3c8Q4y4h3k6U0L8r3W2W2L8Y4c8K6i4@1g2r3i4@1u0o6i4K6S2o6i4@1f1@1i4@1t1^5i4K6S2n7i4@1f1@1i4@1u0m8i4K6R3$3i4@1f1@1i4@1t1^5i4K6R3H3i4@1f1^5i4@1t1%4i4@1q4r3h3f1g2e0i4@1f1#2i4@1q4q4i4K6R3&6i4@1f1#2i4@1p5#2i4@1u0p5i4@1f1#2i4@1t1H3i4@1t1I4i4@1f1#2i4K6S2r3i4@1q4r3i4@1f1$3i4K6S2o6i4@1p5K6i4@1f1&6i4K6V1J5i4@1t1I4i4@1f1K6i4K6R3H3i4K6R3J5i4@1f1K6i4K6R3H3i4K6R3J5i4@1f1K6i4K6R3H3i4K6R3J5i4@1f1K6i4K6R3H3i4K6R3J5

要四部才能完成：

1.Sieving   
2.Auxiliary data gathering
3.Linear algebra
4.Factorization

二次筛选法的工作原理

99bK9s2c8@1M7q4)9K6b7g2)9J5c8W2)9J5c8X3u0T1M7#2)9J5k6h3g2E0j5i4c8Z5i4K6u0W2j5h3y4Q4x3X3g2U0L8W2)9J5c8Y4c8Z5M7X3g2S2k6q4)9J5k6o6p5@1x3K6W2Q4x3X3b7I4i4K6u0V1x3g2)9J5k6h3S2@1L8h3H3`.

用二次筛选法对一个数字 n 进行因数分解，就是要找到两个数字 x 和 y ，它们模 n 之后不相等，并且 x 和 -y 模 n 之后也不相等，但是 x 2 =y 2 (mod n) 。如果找到了这两个数字，那么就可以说 ( x+ y) ( x- y) = 0 (mod n) 。因此 x+ y 和 x- y 就一定与 n 具有相同的非平凡因数。

用二次筛选法进行因数分解有赖于是否能够找到一组数字，这组数的因数可以表示为一些预先选择的素数的乘积。然后用幂向量的形式将这些因数记录下来。一旦具备了足够多的向量，就可以构造一个包含线性依赖关系的集合。用这种线性依赖关系就可以找到两个平方后模 n 相等的数字。

为实现这一目标，二次筛选方法使用了一个素数集合，称作因数基（ factor base）。然后，搜索出那些可以完全分解成这个因数基中的素数的数字。如果因数基中有 k 个素数，那么每一个可分解为因数基中素数的数字就存储为一个 k 维的向量，向量 y 中的第 i 个项表示因数基中第 i 个素数在 y 因数分解结果当中的幂。

最后进行筛选操作，找出 f( r) = r 2 - n 的那些值，而这些值因数分解的结果完全包含在这个因数基中。然后像 Dixon 因数分解法中那样应用高斯消除法，找出是某数的完全平方的一组 f( r) 。

难，贴着慢慢琢磨。。。

3edK9s2c8@1M7q4)9K6b7g2)9J5c8W2)9J5c8X3#2S2k6$3#2S2i4K6u0W2L8h3q4@1K9s2y4Q4x3X3g2#2M7%4W2V1i4K6u0W2k6h3c8#2i4K6u0W2j5i4g2Q4x3V1k6E0j5h3N6E0j5g2)9J5c8X3S2S2L8X3c8T1L8$3!0C8i4K6u0r3N6r3g2^5N6q4)9J5c8U0p5$3y4R3`.`.

[推荐]推荐PARI和SAGE和MXGMA
可用time 看速度：

Z := IntegerRing();
n := 123456789011111222222222455555555555999999999999999999999999999999999999999999999999999999999999999999999999999999999;

time Factorization(n);
time PollardRho(n) ;
time Divisors(n);
time PartialFactorization([n]);
time CoprimeBasis(([ 1, 8961811, 170036731, 1523837046279841, 81017054489197218714231866471,
726059530108887015842608997490338981, 13775875100591969884460009750757346301,
123456789011111222222222444444444444411111111 ]
));

[ <4493, 1>, <1866358739047092109, 1>, <3233066218483497821, 1>,
<4553746329843002811944884231128063084716920766552412595314945012903616003987,
1> ]
Time: 5.690
[ <4493, 1> ]
[ 27477584912332789277147219130993891831738259514800801246383262853327398174938\
793679056309815268194969953260627643 ]
Time: 0.010
[ 1, 4493, 1866358739047092109, 3233066218483497821, 8385549814538584845737,
14526166519646355709753, 6034061390784611392275850413087794489,
27111037828795258985495395906003460639077,
4553746329843002811944884231128063084716920766552412595314945012903616003987,
2045998225998461163406836485045838743963312500411998979075004794297594670591359\
1, 8498924258106110314598224912416571356509386353570039615682567850288675773618\
059783746900238583, 14722563426558624062843851217253269088818827496734439080768\
194963873985715008238232114441812327, 38185666691670753643489824531487655104796\
672886590187993261777351347020250865942608374822771953419,
6614847747552789791435742351911893801606299194282783478989149997268581781753201\
4376890187062785211, 2747758491233278927714721913099389183173825951480080124638\
3262853327398174938793679056309815268194969953260627643,
1234567890111112222222224555555555559999999999999999999999999999999999999999999\
99999999999999999999999999999999999999 ]
Time: 0.010
[
    [
        [],
        [ <12345678901111122222222245555555555599999999999999999999999999999999\
        9999999999999999999999999999999999999999999999999, 1> ]
    ]
]
Time: 0.000
[ <8961811, 4>, <170036731, 4>, <81017054489197218714231866471, 4> ]
Time: 0.000

[推荐]推荐PARI和SAGE和MXGMA
整数分解：PollardRho和Cremona 算法，快100位了

Z := IntegerRing();
n := 1234567890111112222222224555555555559999999999999999999999999999999999999999999999999999999999999999999999999999999994444444444441122222222222222222222111111777;

Factorization(n);
PollardRho(n) ;
Divisors(n);
PartialFactorization([n]);

[ <37, 1>, <3336669973273276276276282582582582594594594594594594594594594594594\
5945945945945945945945945945945945945945945945945795795795795706006006006006006\
006003003021, 1> ]
[ <37, 1>, <3336669973273276276276282582582582594594594594594594594594594594594\
5945945945945945945945945945945945945945945945945795795795795706006006006006006\
006003003021, 1> ]
[]
[ 1, 37, 3336669973273276276276282582582582594594594594594594594594594594594594\
5945945945945945945945945945945945945945945945795795795795706006006006006006006\
003003021, 12345678901111122222222245555555555599999999999999999999999999999999\
9999999999999999999999999999999999999999999999999444444444444112222222222222222\
2222111111777 ]
[
    [
        [],
        [ <12345678901111122222222245555555555599999999999999999999999999999999\
        99999999999999999999999999999999999999999999999994444444444441122222222\
        222222222222111111777, 1> ]
    ]
]
[ <8961811, 4>, <170036731, 4>, <81017054489197218714231866471, 4> ]

[推荐]推荐PARI和SAGE和MXGMA
整数分解：PollardRho和Cremona

Z := IntegerRing();
n := 1234567890111112222211111111888888888888888888888888888888888888888888888888888888888888882222244444444444441122222222222222222222111111;

Factorization(n);
PollardRho(n) ;
Divisors(n);
PartialFactorization([n]);
CoprimeBasis(([ 1, 8961811, 170036731, 1523837046279841, 81017054489197218714231866471,
726059530108887015842608997490338981, 13775875100591969884460009750757346301,
123456789011111222222222444444444444411111111 ]
));