在逆向分析的过程中，我们经常会遇到一些常用的已公开的算法如md5、sha1、sha256、sm3、base64等，这些算法常用于数据计算或者转换；也经常会遇到另外一些常用的算法如rc4、aes等，而这些算法常用于数据加密，所有这些算法都是用于特定安全场景（保密性、完整性）的，今天我们要分享的主题是当逆向过程中遇到这些算法的时，我们如何快速的识别这些算法，特别是在分析汇编级别的程序时尤为有用（现在安全能力越来越强，即使是编译后的汇编程序也可能进行了各种加固，让我们不能直观的分析程序）。

       抛开各种算法背后的数学和密码学原理（作为逆向工程师，我们不要陷入其中），快速识别算法才是最重要的，它能大大的节省我们分析应用逻辑的时间，今天我们着重介绍一下md5、sha1、sha256、sm3、aes这样算法的识别，对剩下的base64、rc4算法识别我们将放到下一篇文章中。

在陈述本篇文章前，我先介绍一下本篇识别算法的方法-常数识别法和S-box(inv-sbox)识别法。

或许这些方法早已在高级逆向工程师中传播(更多的是高级逆向工程师的自我发现和觉醒，形成的自我经验，或许他们不愿意传播)，但对于刚刚研究和学习逆向或者中级逆向工程师来说它了解它们是有裨益的。

已公开的通用的哈希算法，在程序运算的开始都会初始化固定数量的常数，考虑到算法的复杂性，一般这些算法不会被修改，因此识别这些常数就成了我们识别算法的关键。

           同样已公开的某些加密算法也具备这样的特征，如aes、des这样的算法，它们算法中通常包含一个固定的默认 S-box（Substitution box）。它是 字节替换（SubBytes）步骤 中使用的查表，用于把每个字节替换成另一个字节，从而实现非线性变换。识别S-box就成了识别这类加密算法的关键。

Inv-sbox同理。

md5算法的识别属于常数识别范畴，它包含以下4个有且只有4个常数（区别于sha1），要仔细核对常数个数：

A = 0x67452301，B = 0xefcdab89，C = 0x98badcfe，D = 0x10325476

我手边有js实现的md5代码，我们来截取一部分看一下：

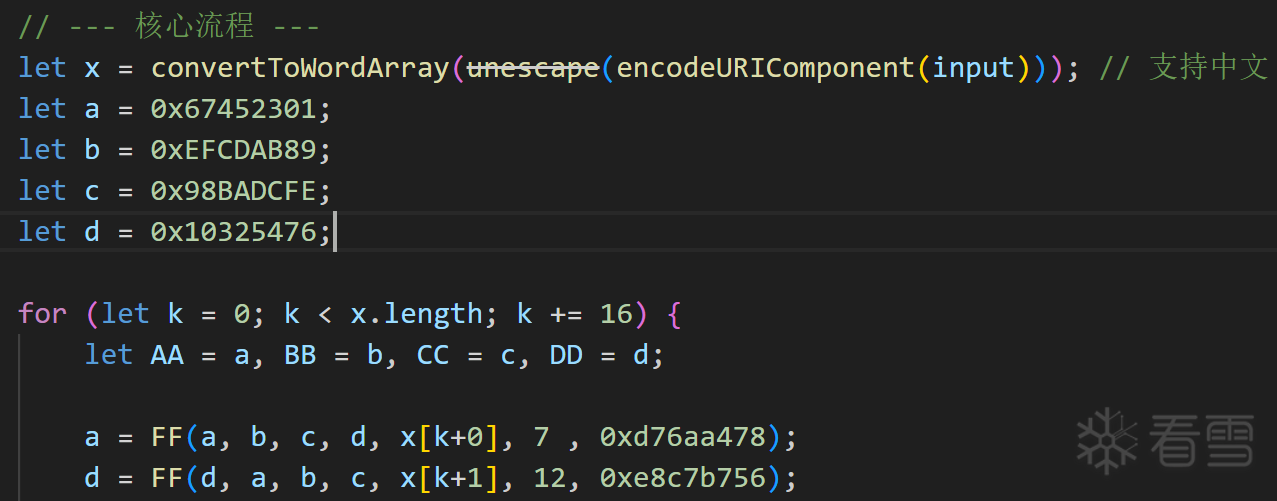
那我们看一下包含md5算法的汇编程序（利用反编译软件）：

这幅图片是包含md5算法的4个常量的地方，通过交叉引用我们可以找到它们被引用的地方。

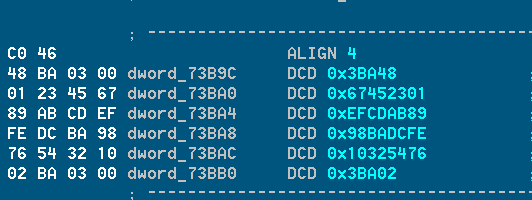
即下面这幅图，该程序是md5算法的主体，它包含了上面4个常数，并且它确实是md5。

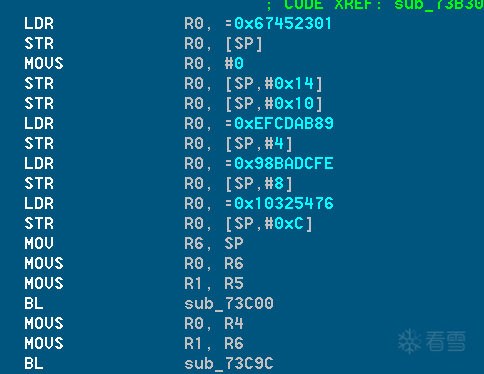
sha1算法的识别属于常数识别范畴，它包含以下5个有且只有5个常数，它的前4个常数和md5算法常数完全相同，因此在识别该算法的时候一定要仔细查看常数的个数：

H0 = 0x67452301，H1 = 0xEFCDAB89，H2 = 0x98BADCFE，H3 = 0x10325476，H4 = 0xC3D2E1F0

识别方法同md5，这里就不再给大家演示了。

sha256算法的识别属于常数识别范畴，它包含以下8常数：

H0 = 0x6A09E667

H1 = 0xBB67AE85

H2 = 0x3C6EF372

H3 = 0xA54FF53A

H4 = 0x510E527F

H5 = 0x9B05688C

H6 = 0x1F83D9AB

H7 = 0x5BE0CD19

识别方法同md5，这里就不再给大家演示了。

sm3算法的识别属于常数识别范畴，它包含以下8常数（很容易和sha256混淆）：

A=0x7380166F

B=0x4914B2B9

C=0x172442D7

D=0xDA8A0600

E=0xA96F30BC

F=0x163138AA

G=0xE38DEE4D

H=0xB0FB0E4E

识别方法同md5，这里就不再给大家演示了。

       所有标准 AES（AES-128 / AES-192 / AES-256）都使用同一个 S-box。它是固定的，不会在算法运行时“随机生成”或“动态变换”。

S-box如下（固定的 16×16 表）：

0

1

2

3

4

5

6

7

8

9

A

B

C

D

E

F

0x0

63

7C

77

7B

F2

6B

6F

C5

30

01

67

2B

FE

D7

AB

76

0x1

CA

82

C9

7D

FA

59

47

F0

AD

D4

A2

AF

9C

A4

72

C0

0x2

B7

FD

93

26

36

3F

F7

CC

34

A5

E5

F1

71

D8

31

15

0x3

04

C7

23

C3

18

96

05

9A

07

12

80

E2

EB

27

B2

75

0x4

09

83

2C

1A

1B

6E

5A

A0

52

3B

D6

B3

29

E3

2F

84

0x5

53

D1

00

ED

20

FC

B1

5B

6A

CB

BE

39

4A

4C

58

CF

0x6

D0

EF

AA

FB

43

4D

33

85

45

F9

02

7F

50

3C

9F

A8

0x7

51

A3

40

8F

92

9D

38

F5

BC

B6

DA

21

10

FF

F3

D2

0x8

CD

0C

13

EC

5F

97

44

17

C4

A7

7E

3D

64

5D

19

73

0x9

60

81

4F

DC

22

2A

90

88

46

EE

B8

14

DE

5E

0B

DB

0xA

E0

32

3A

0A

49

06

24

5C

C2

D3

AC

62

91

95

E4

79

0xB

E7

C8

37

6D

8D

D5

4E

A9

6C

56

F4

EA

65

7A

AE

08

0xC

BA

78

25

2E

1C

A6

B4

C6

E8

DD

74

1F

4B

BD

8B

8A

0xD

70

3E

B5

66

48

03

F6

0E

61

35

57

B9

86

C1

1D

9E

0xE

E1

F8

98

11

69

D9

8E

94

9B

1E

87

E9

CE

55

28

DF

0xF

8C

A1

89

0D

BF

E6

42

68

41

99

[培训]Windows内核深度攻防：从Hook技术到Rootkit实战！