LLM 还是有极限的，还是人脑子好使（虽然高考完三个月脑子就没动过 导致好久才转过来弯 悲

先用错误的 Flag 试一遍，看下程序输出

拉进 IDA，发现这些字符串并不存在，那就直接拉进 x64dbg，在输入 flag 前按下暂停，从堆栈找 mainFunc (0x140057A20)

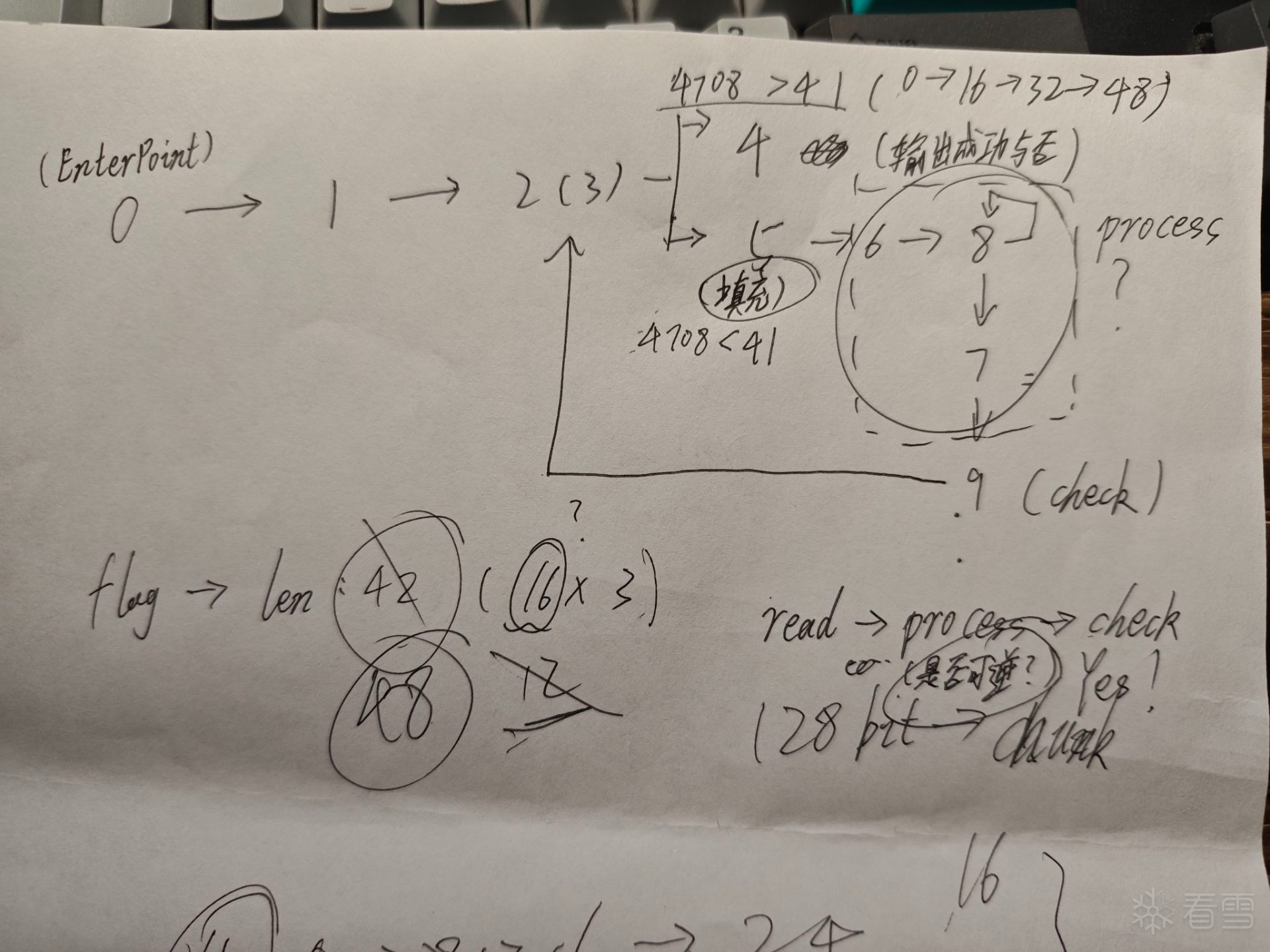
通过对 mainFunc (0x140057A20) 伪代码 switch-case 结构的分析，得到下面的操作流程

其中，case 5 会在一开始将a1 + 4580全部初始化为 0x2

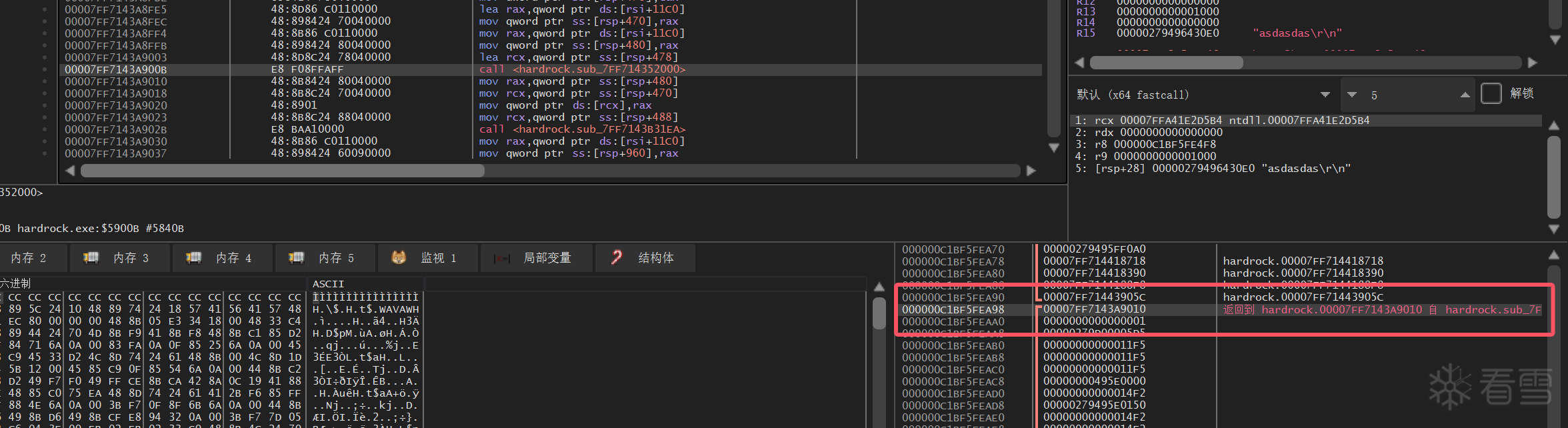
然后将用户输入按照每 16 字符一次的顺序，将字符转化为 int (所以 a1 + 4580 和 a1 + 4718 这两个的大小都是 16 * 8 = 128 byte)

然后根据int对应的二进制将其映射，映射规则为 0 -> 0x2, 1 -> 0x3

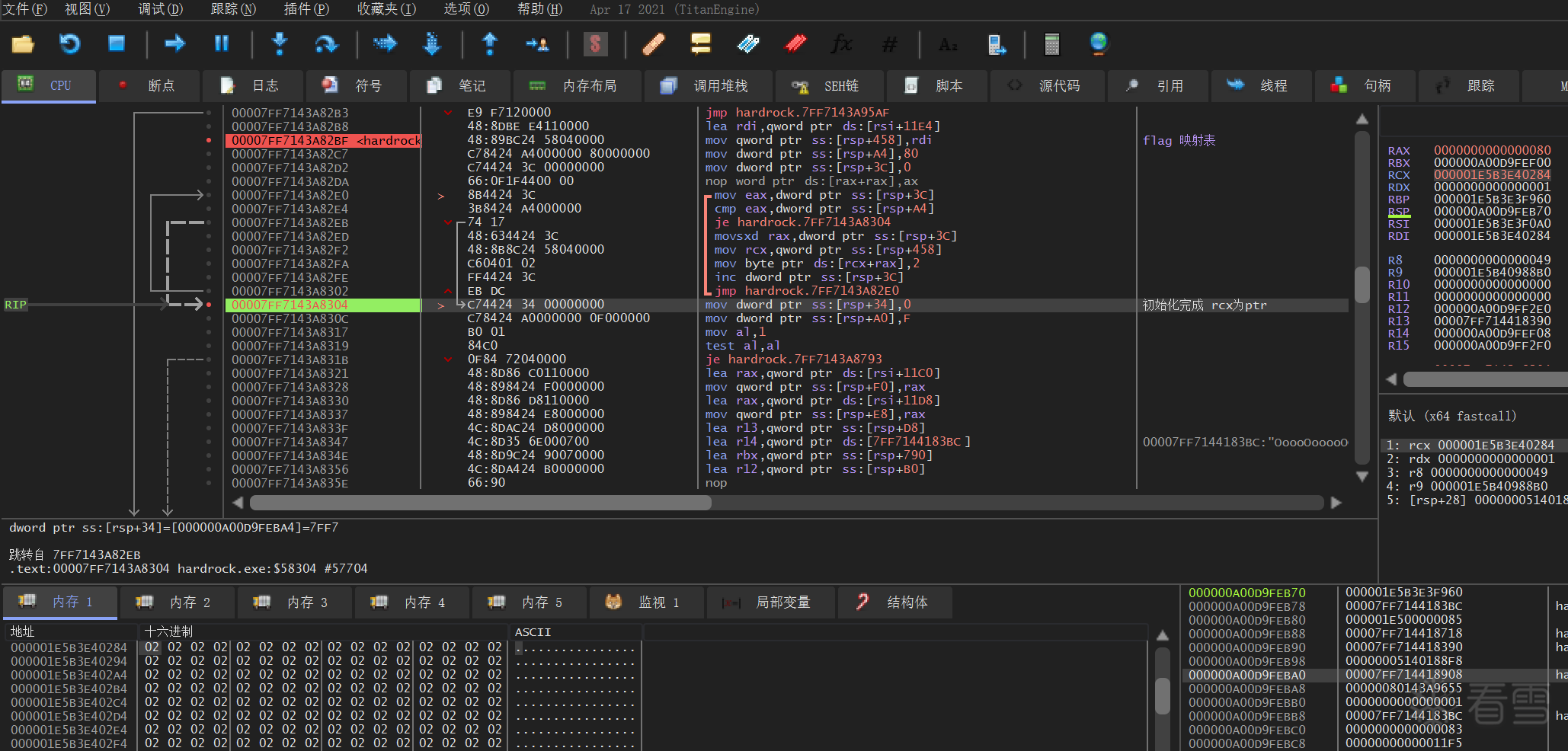
这就是一个把整数 a2 按位拆成长度为 a3 的二值序列的函数，且0 位写成字节 2，1 位写成字节 3。它从 LSB→MSB 逐位取模/整除 2，并把结果右对齐写进输出缓冲（索引是 width-1-pos），超出 a3 还剩下非零高位会被当成错误处理（设置特殊的 vtable/类型标记）。伪代码还原如下（变量名照反编译语义化）：

最后把映射后的值填充到 a1 + 4580 和 a1 + 4718 中, 我们称这个原始映射为 p1​

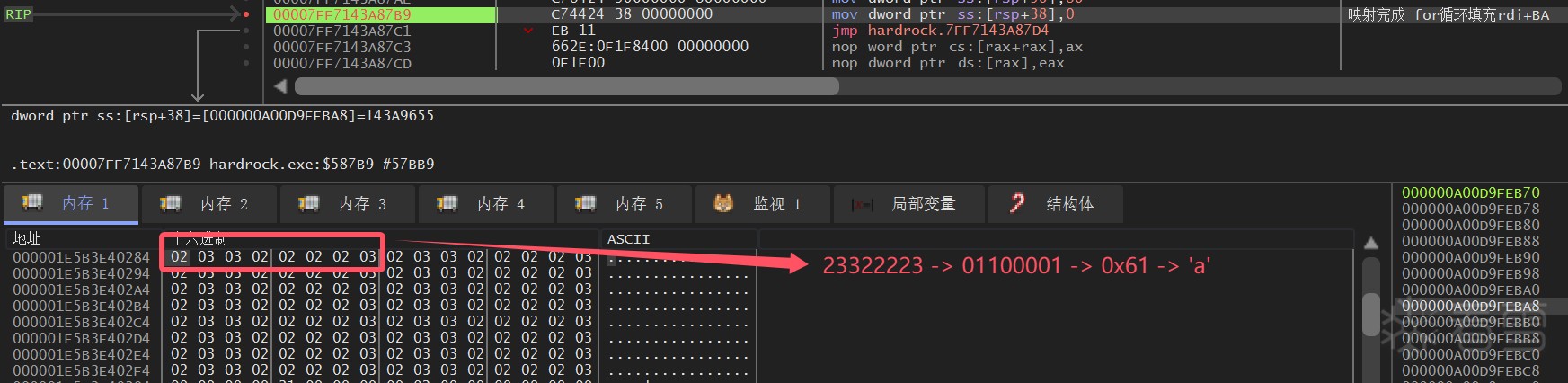
在经过case 6/8/7后, p1​ 会根据一定计算生成最终用于比较的 p2​, 而 p2​ 的值是不等于 p1​ 的

在case 9中，会将 p2​ 与预定好的 byte_1400C89D0 比较，如果比较结果 a1 + 4576 大于等于42，那么在case 4就会输出Correct!，反之输出 Wrong! (从 a1 + 4576 也可以看出 Flag 长度应该为 42)

同时 case 3 -> case 5 -> case 6/8/7 -> case 9 -> case 3 的这个循环一共会经历三次，这个三次循环是由 a1 + 4708 决定的，而 a1 + 4708 由 case 9 赋值，可以得到 a1 + 4708 的变换为 0 -> 16 -> 32 -> 48 (跳入 case 4)

在经历了12小时逆不出来 p1​ 到 p2​ 的算法之后，我人已经麻了(╬▔皿▔)╯

后来想了一下，有人能够1h就做出来，绝壁有简单的解法

在推 mainFunc 逻辑的时候，我猜想 p1​ 到 p2​ 的算法会不会是可逆的（不要管旁边那个 Yes, 那是做出来之后写的【】）
（另外是byte不是bit，半夜脑子不清楚了）

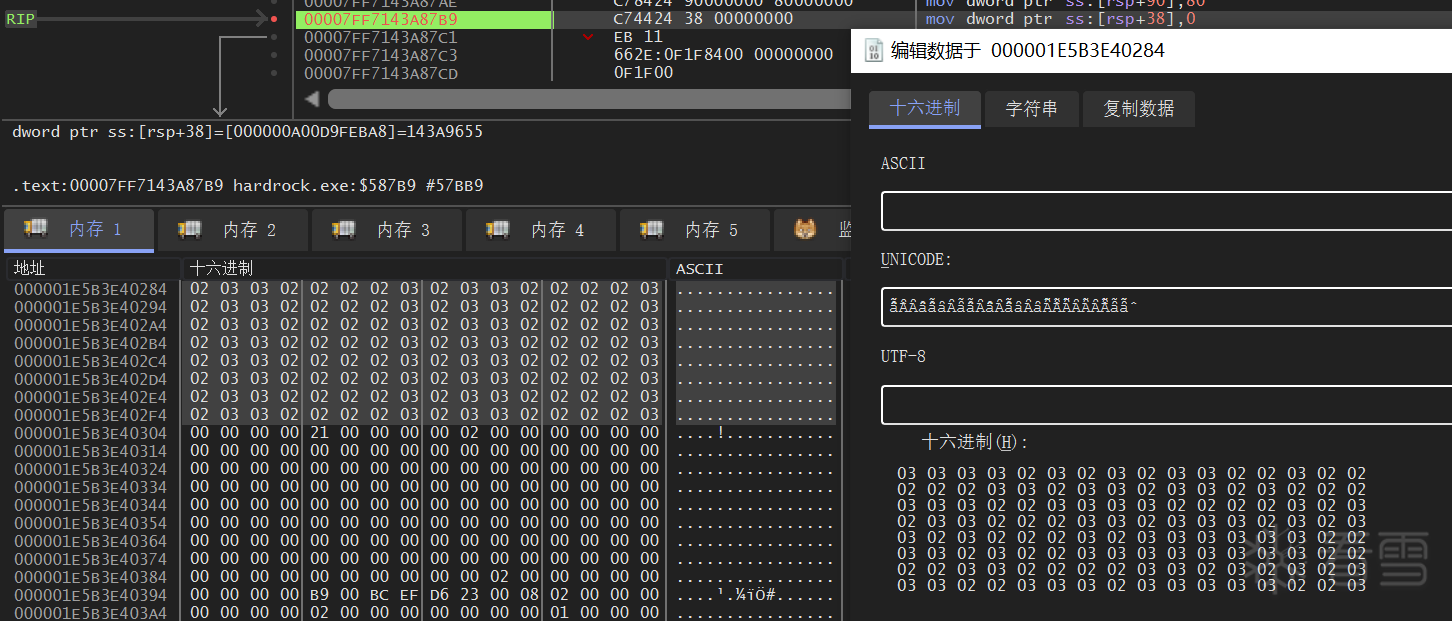
于是我将 byte_1400C89D0 导出，用 Python 分割为 128 byte 的三个片段，在 x64dbg 动调的时候把 a1 + 4580 里面的映射替换掉

在 x64dbg 里面选中内存，Ctrl+E 进入编辑页面，将片段直接粘贴保存

最后在 case 9 dump这段 p1​ 对应的 p2​

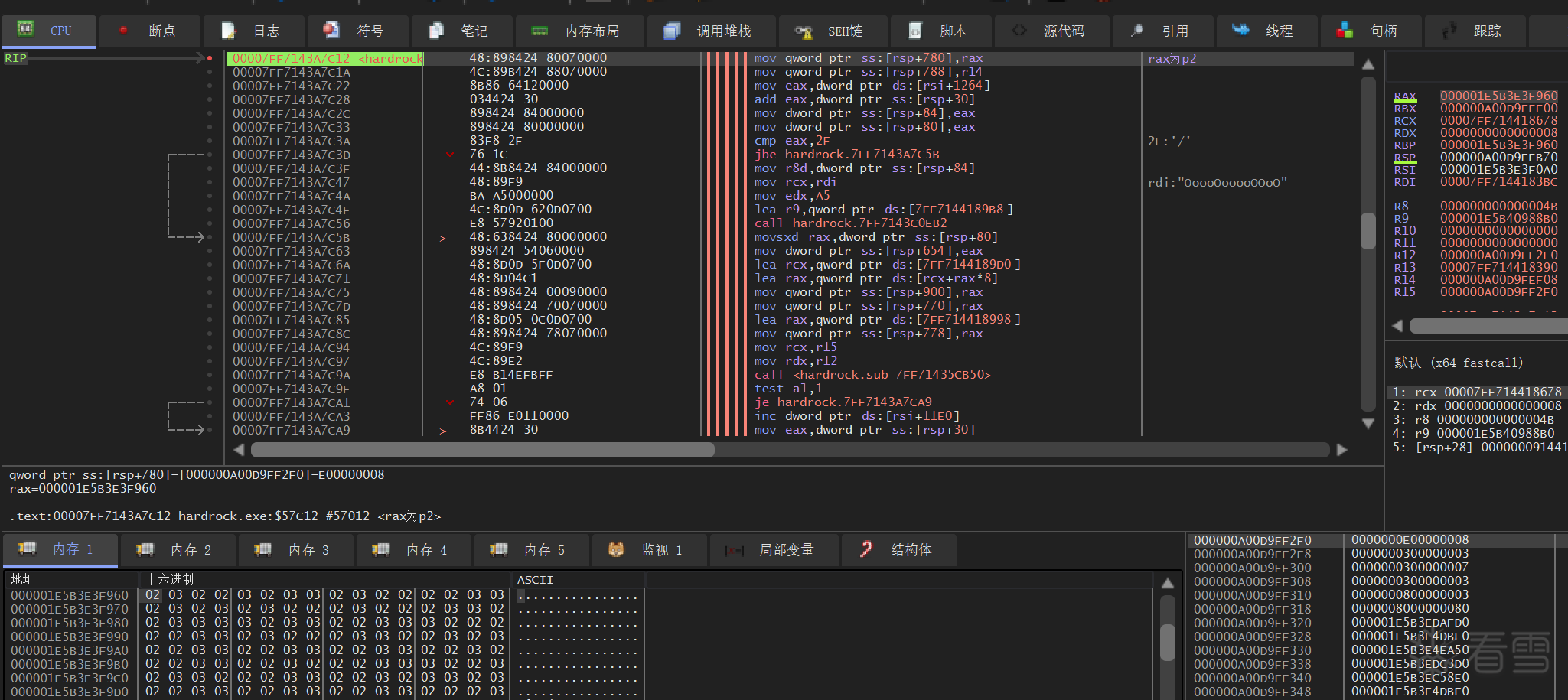
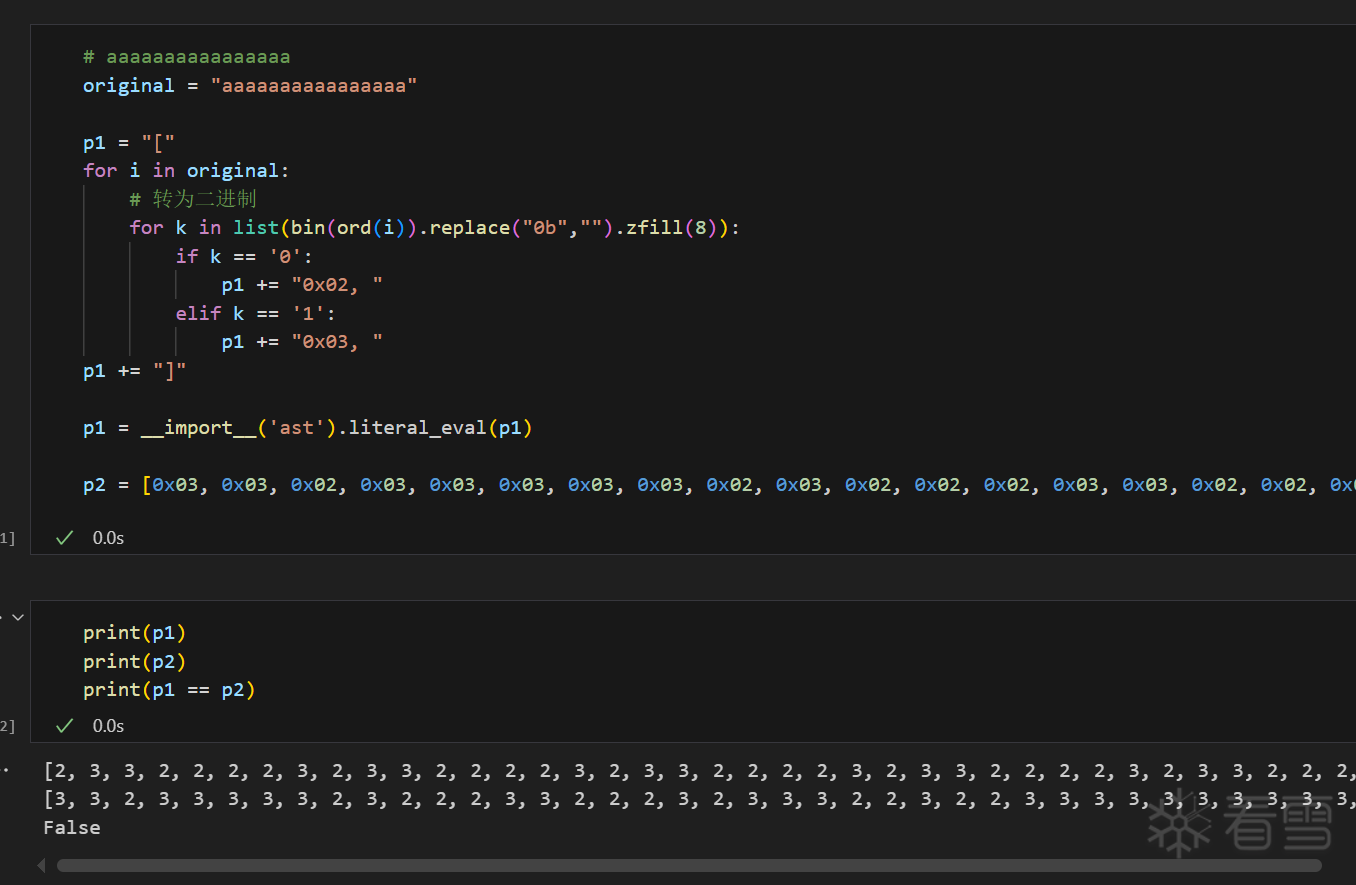
（上为 p1​，下为 p2​）

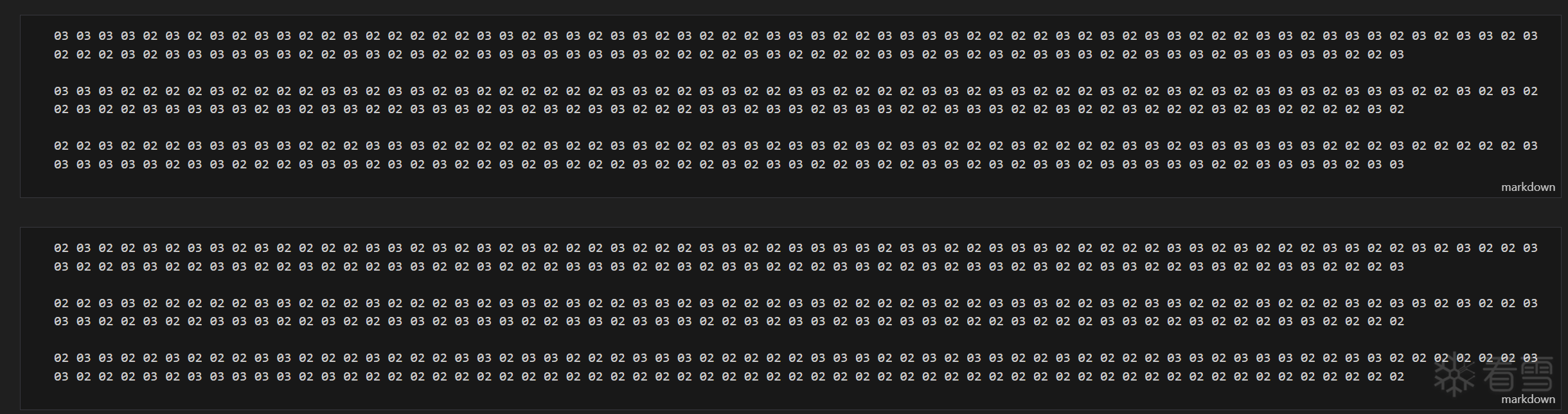
最后将 p2​ 转化为字符串，得到 Flag

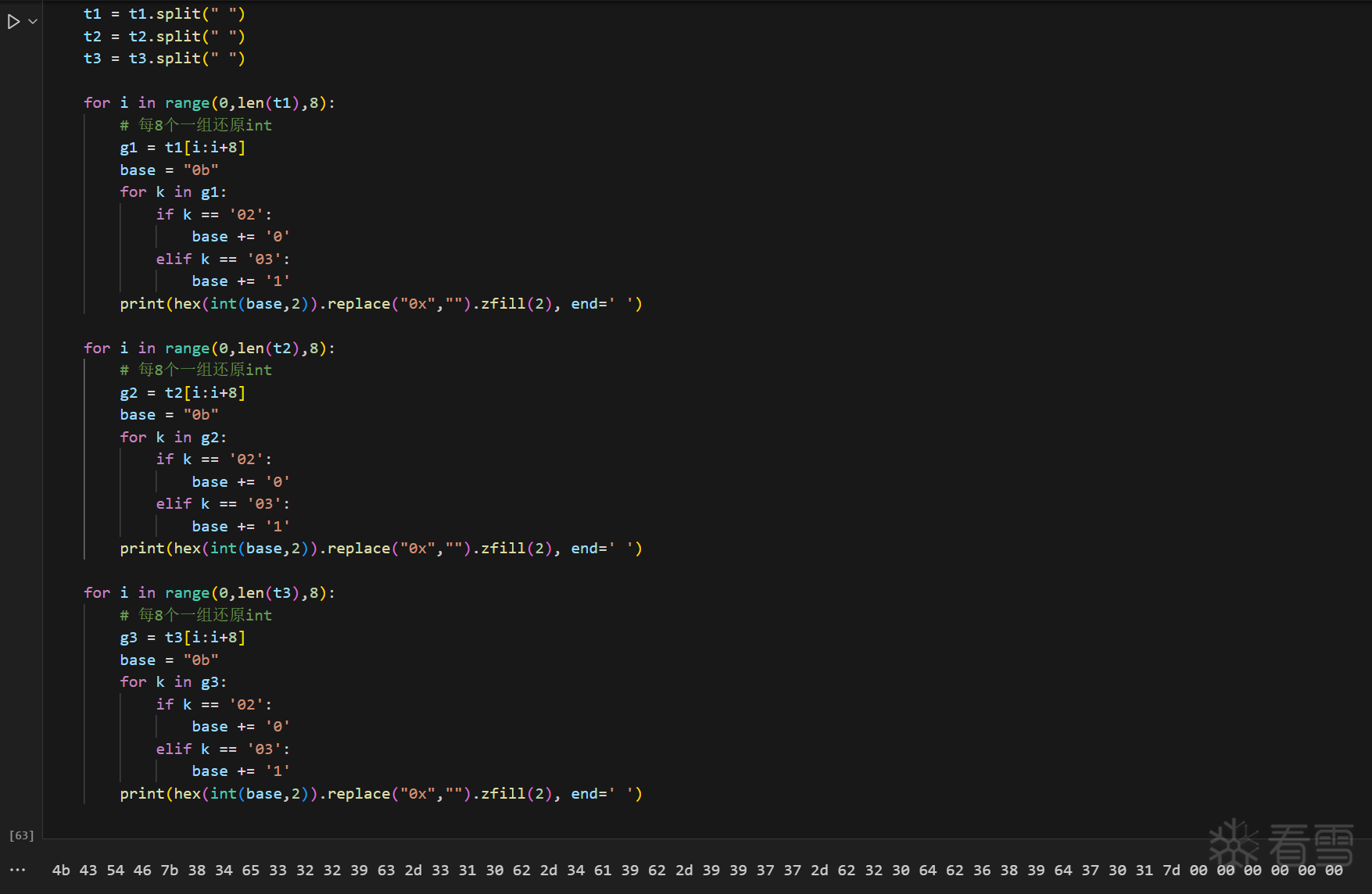
于是我们也可以得到一个结论，即 p1​ 到 p2​ 是可逆的，可以从已知的 p2​ 倒退回用户输入的 p1​

最后可得到 Flag 为 KCTF{84e3229c-310b-4a9b-9977-b20db689d701}

中间有几道题没做是因为偷懒了，也没进前 10（我的T恤啊啊啊啊啊啊啊
（首）

传播安全知识、拓宽行业人脉——看雪讲师团队等你加入！