以前写了篇RSA的量子算法分析的文章，在这篇文章里留了个离散对数问题的坑一直没填，借此机会把坑填了，ECC的shor算法破解除了少数几篇论文中简单地提及外，几乎没有系统而详细地资料，本文算是独一篇了。我们知道RSA算法的安全是基于大数质因数分解难题，即RSA的安全性主要依赖于从两个大素数的乘积中恢复这两个素数的难度。而椭圆曲线密码学(ECC)主要依赖于离散对数问题的难解性上。不过用Shor算法的思想来破解ECC相对来说要困难些：算法设计会更复杂，量子电路复杂度也会更高，并且需要更多的量子比特（目前对于如何降低量子比特数依然是量子计算前沿的重要课题，比如如何优化量子电路减少量子比特以及如何实现高效的量子纠错机制从而减少量子比特数）。因此本文稍微会比RSA那篇要难理解点，不过这篇尽量保证严谨的基础上更通俗易懂。

在之前的文章中我们比较详细地讨论了利用Shor量子算法攻破RSA加密体系的核心思想和实现过程，也在该篇文章中点破了RSA的脆弱性本质：即周期性（依赖于模幂运算的RSA算法必然具备周期性）。而Shor量子算法便是这种“周期性漏洞”的量子攻击武器。本文中，我们将使用这项“量子武器”来破解椭圆曲线加密算法并对整个攻击过程进行深入的分析。

椭圆曲线密码学（Elliptic Curve Cryptography，简称ECC）是一种基于椭圆曲线数学结构的公钥加密技术，与传统的RSA密码系统相比，ECC能够在远短的密钥长度下提供同等甚至更高的安全性。例如，一个256位的ECC密钥提供的安全强度，大致相当于一个3072位的RSA密钥。因此ECC特别适合在计算能力、存储空间和带宽受限的环境中（如移动设备、物联网芯片和区块链系统）使用，目前被广泛应用于数字签名（ECDSA）、密钥交换（ECDH）和加密传输等关键领域。

在分析分析量子破解前，有必要简单介绍一下椭圆曲线以及其数据加密的基本原理，首先椭圆曲线是一些列满足以下方程的曲线：

$y^{}=x^{}+ax+b(a^{}+b^{}\ne )$y2=x3+ax+b(4a3+27b2=0)

其中，参数a 和 b是定义曲线的常数，并且必须满足 $a^{}+b^{}\ne$4a3+27b2=0 以确保曲线没有奇点（即曲线是光滑的）。对于比较简单的椭圆曲线 $y^{}=x^{}-x+$y2=x3−x+1 ，大概长这样。

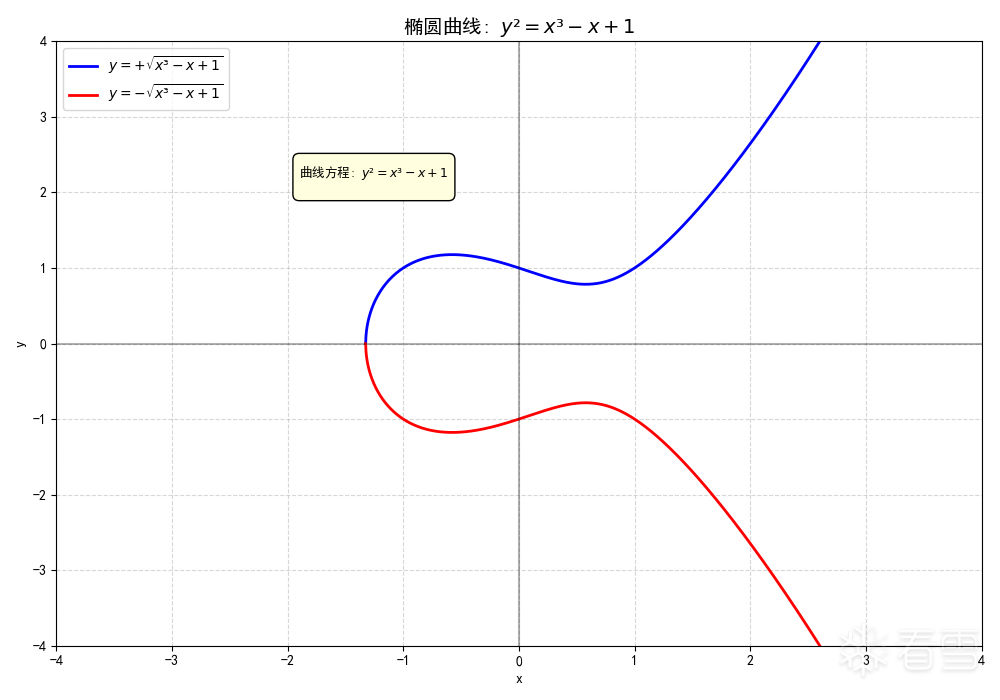
为了利用椭圆曲线的特性来构造非对称加密，我们首先需要在椭圆曲线上定义点的加法和标量乘法运算。

点加运算：两点 P 和 Q 的加法结果是曲线上另一点 R，即 $P+Q=R$P+Q=R 。若 $P=(,),Q=(,)R=(,)$P=(x1​,y1​),Q=(x2​,y2​)，R=(x3​,y3​) ，则 $P+Q=(,)$P+Q=(x3​,y3​) ，计算方式如下：

⎩⎨⎧​λ=x2​−x1​y2​−y1​​λ=2y1​3x12​+a​x3​=λ2−x1​−x2​,y3​=λ(x1​−x3​)−y1​​(P=Q)(P=Q)​

标量乘法：通过点加运算，我们可以构造标量乘法（我们利用标量乘法的困难性来保证密码学的安全性），如：

$\cdot P=P+P\cdot P=P+P+Pk\cdot P=P+P+P+...$2⋅P=P+P；3⋅P=P+P+P；k⋅P=P+P+P+... 。

注意，我们定义椭圆曲线上的点加运算和标量乘法运算，是为了构建一个代数结构（群），从而使得椭圆曲线可以用于密码学。具体来说，椭圆曲线上的点加上一个特殊的“无穷远点”构成一个阿贝尔群（交换群）。

比如点加运算定义了椭圆曲线上两个点相加的几何和代数规则，结果仍然是曲线上的点。这个运算满足群的性质（封闭性、结合律、单位元、逆元、交换律）。

而标量乘法中，我们通过重复点加运算，可以定义整数k与点P的乘法，即k个P相加。这是椭圆曲线密码学（ECC）中的核心运算，因为从公钥（点Q）和基点G恢复私钥k（整数）的困难性（椭圆曲线离散对数问题）保证了安全性。

阶的计算：对于有限域的椭圆曲线，我们可以选取曲线上的一个点作为基点，然后不断累加直到得到无穷远点O，这个累加到点O需要的次数我们称为该基点的阶。比如我们选择一条定义在有限域 $$F11​上的椭圆曲线: $y^{}=x^{}+x+\left(\right)$y2=x3+x+6 (mod 11) ，然后我们选择曲线上的一个点作为基点 $G=(,)$G=(2,4) ，接下来依次对基点进行累加直到找到周期，即基点的阶。比如：

$G=G+G=(,)+(,)$2G=G+G=(2,4)+(2,4)。先计算斜率： $s=(\times {}^{}+)/(\times )=/\equiv \times {-}^{}\equiv \times \equiv \left(\right)$s=(3×22+1)/(2×4)=13/8≡2×8−1≡2×7≡3 (mod 11)，然后得到 $G$2G 的坐标：$={}^{}--=$x3​=32−2−2=5，$=(-)-=-\equiv$y3​=3(2−5)−4=−13≡9*，所以 *$G=(,)$2G=(5,9)

$G=G+G=(,)+(,)$3G=2G+G=(5,9)+(2,4)。 计算斜率：$s=(-)/(-)=/\equiv \ast =\equiv \left(\right)$s=(4−9)/(2−5)=5/3≡5∗4=20≡9(mod 11)。然后计算点坐标 ：$={}^{}--=\equiv$x3​=92−5−2=74≡8 ，$=(-)-=-\equiv$y3​=9(5−8)−9=−36≡8 ，所以 $G=(,)$3G=(8,8)。

继续计算下去，最终会发现点 $(,)$(2,4) 的阶是 $$13 （即 $G=O$13G=无穷远点O ）。

1G = (2, 4)，2G = (5, 9)，3G = (8, 8)，4G = (10, 9)，5G = (3, 5)，6G = (7, 2)，7G = (7, 9)，8G = (3, 6)，9G = (10, 2)，10G = (8, 3)，11G = (5, 2)，12G = (2, 7)，13G = O (无穷远点), 14G = (2, 4), 15G = (5, 9)

我们还可以看出，如果点 $G$G 的阶为 $n$n ，那么有: $G=(n+)G$G=(n+1)G 。

基于以上运算法则，我们就可以实现ECC的加解密，过程如下：

第一步生成密钥： 选择椭圆曲线 $E$E 和基点 $G$G ，基点$G$G的阶为质数 $n$n 。 生成小于 $n$n 的随机整数 $k$k 作为加密私钥。我们在通过私钥k和基点G来生成公钥 $Q$Q 即 $Q=k\cdot G$Q=k⋅G 。

第二步加密明文： 将明文编码为曲线上的点 M。 选择随机数（ r<n ）。 然后通过公钥 $Q$Q 计算得到密文对 ( $Cipher,Cipher$Cipher1,Cipher2 )： $Cipher=M+r\cdot QCipher=r\cdot G$Cipher1=M+r⋅Q，Cipher2=r⋅G 。

第三步解密密文： 有了密文对后，我们可以通过私钥解密密文得到明文： $M=Cipher-k\cdot Cipher=M+r\cdot Q-k\cdot r\cdot G=M+r\cdot Q-r\cdot k\cdot G=M+r\cdot Q-r\cdot Q=M$M=Cipher1−k⋅Cipher2=M+r⋅Q−k⋅r⋅G=M+r⋅Q−r⋅k⋅G=M+r⋅Q−r⋅Q=M

椭圆曲线密码学（ECC）的安全性建立在椭圆曲线离散对数问题（即ECDLP） 的难解性上，其核心是标量乘法计算上的严重不对称性，即正向计算容易，逆向求解极难。具体而言，在当前ECC加密算法中，已知公开的基点 G 和通过标量乘法得到的公钥 $Q=k\cdot G$Q=k⋅G ，想要逆向推导出私有密钥 k所需要的计算量远远高于人类计算的极限。目前，已知最有效的用于求解ECDLP的经典算法（如Pollard Rho算法）所需要的时间复杂度也是指数级或亚指数级的。Pollard's Rho算法计算私钥需要的时间复杂度为 $O\left(\right)$O(2n​) ，其中 $n$n 为私钥比特位长度，比如当私钥长度k为 $n=$n=256 位时，该算法需要 ${}^{}$2128 次计算，即使在宇宙年龄（${}^{}$1017 秒）尺度下，也需要每秒 ${}^{}$10111 次的计算。虽然这是一个恐怖的计算量，但对于量子计算机而言，通过巧妙地设计一套算法，就可以让这种完全不可能的任务变得轻松且简单（将复杂度降至多项式级$O\left(\right(logn{)}^{})$O((logn)3)）。

在之前文章中，我们通过构建Shor量子算法来寻找RSA代数结构中的周期，进而实现合数的因式分解。而构造Shor算法的本质就是寻找周期，理论上任何一个核心代数结构中存在周期性的加密算法，Shor算法都可以在多项式复杂度下成功地完成攻击。既然定义点加运算和标量乘法的椭圆曲线本质上构成了一个阿贝尔群，那么基于有限域的椭圆曲线加密算法自然也存在一个周期，但在RSA中周期性是比较能够直接发现的，但在ECC中，这个周期性似乎不可见，相对来说比较隐蔽，这就需要我们通过特定的方式找出来。这个特定的方法就引入二元函数，通过简单的变换就可以观察到这个函数在二维平面上的周期。我们定义函数：

$f(a,b)=a\cdot G+b\cdot Q$f(a,b)=a⋅G+b⋅Q ，

代入 $Q=k\cdot G$Q=k⋅G 可得：

$f(a,b)=(a+b\cdot k)\cdot G$f(a,b)=(a+b⋅k)⋅G

我们设 $f(a,b)$f(a,b) 的周期为 $(,)$(ar​,br​) ( $,$ar​,br​ 为整数),因此有：

$f(a,b)=f(a+,b+)=(a+b\cdot k+(+\cdot k\left)\right)\cdot G\Rightarrow +\cdot k=$f(a,b)=f(a+ar​,b+br​)=(a+b⋅k+(ar​+br​⋅k))⋅G⇒ar​+br​⋅k=0

因此，只要满足此式的任何组合都是函数 $f(a,b)$f(a,b) 的周期。由于 $,,k$ar​,br​,k 皆为整数，因此我们取一个比较好算的周期，设 $=$br​=1 ，则周期对为 $(-k,)$(−k,1) 。也就是说我们让$(a,b)$(a,b) 沿方向 $v=(-k,)$v=(−k,1) 移动，函数 $f$f 值就会不变，验证：

$f(a-k\cdot s,b+s)=(a-ks+(b+s\left)k\right)\cdot G=(a+bk)\cdot G=f(a,b)s\in Z$f(a−k⋅s,b+s)=(a−ks+(b+s)k)⋅G=(a+bk)⋅G=f(a,b)s∈Z

这里 $s$s 为整数，也就是说函数在整数平移 $(a,b)\to (a-ks,b+s)$(a,b)→(a−ks,b+s) 下保持不变。因此，我们通过制备一套量子叠加态系统利用量子纠缠、量子测量以及量子傅里叶变换（QFT），就可以把将 $f(a,b)$f(a,b) 的空间周期性转换为动量空间的尖峰，从而可以迅速地找到 $k$k （加密私钥）。

接下来我们将一步一步地设计并实现这样的量子算法。

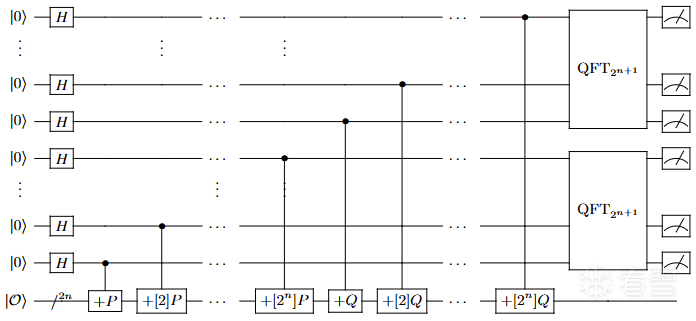
1. 初始化量子寄存器

首先我们需要两个量子寄存器用于存储编码的信息（实际还需要临时存储点加法中间结果，所以需要更多的辅助寄存器，此处简化不考虑）。

寄存器1（reg1）：用于存储椭圆曲线上的点。每个点由两个坐标值(x,y)表示，每个坐标是有限域$$Fp​中的元素。因此，每个坐标值需要log₂p个量子比特来表示，所以总比特数为 $l=lo\left(p\right)$l=2log2​(p)。如果 $p=$p=11 ，那么我们需要8个比特量子寄存器来存储。注意，椭圆曲线密码学中，通常使用压缩表示形式，即只存储x坐标和y的符号位，这样可以节省存储。但在量子计算中，reg1会处于叠加态（无法提前知道点的位置）以及需要进行点加法运算，我们需要完整的坐标，因此存储时无法进行压缩。

寄存器2（reg2）：用于存储整数对$(a,b)$(a,b)。设有限域上的椭圆曲线的阶为 $n$n,由于a和b都在模n的整数环中取值，因此Reg2实际上是两个量子寄存器组合而成。设每个量子比特数为 $t$t ，为了确保在应用QFT时，周期能够以高概率被检测到，所以设 $t^{}\ge n^{}$2t≥2n2 得 $t=lo\left(n^{}\right)$t=log2​(2n2) ，故寄存器Reg2有2t个量子比特。

准备好两个量子寄存器后，我们首先需要对其进行初始化，一般将所有量子态置为 $\mid ⟩$∣0⟩ 。所以，我们这台量子计算机的初始状态为：

$\mid ⟩=\mid {⟩}_{\otimes l}^{}\otimes \mid ,{⟩}_{\otimes t}^{}$∣ψ0​⟩=∣0⟩1⊗l​⊗∣0,0⟩2⊗2t​

其中 $\mid {⟩}_{\otimes l}^{}$∣0⟩1⊗l​ 为 $l$l 个量子比特的寄存器reg1， $\mid {⟩}_{\otimes t}^{}$∣0⟩2⊗2t​ 为 $t$2t 个量子比特的寄存器reg2。

然后，对reg2应用Hadamard变换，使其处于所有可能$(a,b)$(a,b)的均匀叠加态(总共有 $t^{}$22t 个态的叠加)：

$\mid ⟩={\sum }_{a=}^{t^{}-}{\sum }_{b=}^{t^{}-}\mid {⟩}_{\otimes m}^{}\mid a,b$∣ψ1​⟩=2t1​∑a=02t−1​∑b=02t−1​∣0⟩1⊗m​∣a,b⟩2​

2. 实现函数f的量子黑盒（Oracle）

对于我们定义的函数： $f(a,b)=aG+bP$f(a,b)=aG+bP ，由于椭圆曲线点群是阿贝尔群，所以 $aG+bP$aG+bP 也是椭圆曲线上的一个点。我们需要通过设计一个特殊量子电路来计算该函数的结果，该电路需要实现基础的模运算如模加、模减、模乘、模逆运算外，还需要实现更为复杂的椭圆曲线标量乘法以及点加法，为了方便，我们将这一系列量子电路运算单元简化为量子黑盒，定义为 $$Uf​（其中一种较为高效实现方法可以参考：a9dK9s2c8@1M7s2y4Q4x3@1q4Q4x3V1k6Q4x3V1k6W2M7s2u0A6L8Y4c8Q4x3X3g2A6j5h3y4J5i4K6u0W2L8%4u0Y4i4K6u0r3x3U0l9I4y4#2)9J5c8U0f1&6z5q4)9J5k6i4m8V1k6R3`.`.）

通过量子电路可以在量子叠加态上计算函数 $f(a,b)=aG+bP$f(a,b)=aG+bP 的结果，然后将结果存储到寄存器Reg1中。 $$Uf​ 执行操作简单表示如下：

$\otimes =\otimes$Uf​Reg2∣a,b⟩​​⊗Reg1∣0⟩​​=Reg2∣a,b⟩​​⊗Reg1∣aG+bQ⟩​​

因此，应用 $$Uf​ 后，系统状态变为：

$\mid ⟩={\sum }_{a=}^{t^{}-}{\sum }_{b=}^{t^{}-}\mid a,b⟩\mid f(a,b)⟩={\sum }_{a=}^{t^{}-}{\sum }_{b=}^{t^{}-}\mid a,b⟩\mid (a+kb)\cdot G⟩$∣ψ2​⟩=2t1​∑a=02t−1​∑b=02t−1​∣a,b⟩∣f(a,b)⟩=2t1​∑a=02t−1​∑b=02t−1​∣a,b⟩∣(a+kb)⋅G⟩

注意，最后计算得到函数结果存到Reg1中。

3. 测量寄存器1（函数值寄存器）

现在，测量寄存器Reg1，Reg1会随机坍塌到某个 $m$m 值的状态，然后可以计算得到曲线点 $Q=m\cdot G$Q=m⋅G 。由于两个寄存器是处于纠缠态，因此测量Reg1时，寄存器Reg2（存储$(a,b)$(a,b)的寄存器）会坍缩到所有满足 $f(a,b)=Q$f(a,b)=Q 的$(a,b)$(a,b)对的叠加态上，即：

$\mid ⟩=\mid a,b⟩$∣ψ3​⟩=K​1​∑(a,b)∈S​∣a,b⟩

其中 $S$S 是满足 $aG+bP=Q$aG+bP=Q 的所有 $(a,b)$(a,b) 的集合。其中， $K\approx t^{}/n$K≈22t/n 是满足等式$Q=m\cdot G$Q=m⋅G的$(a,b)$(a,b)对的有效态数量。如果我们固定b，则a分布在模n意义下具有周期性，解a被确定为 $a=(m-bk)modn$a=(m−bk) mod n 。但是，由于我们的寄存器reg2中a和b的取值范围是0到 $t^{}-$2t−1 （而不仅仅是0到n-1），所以对于每个b，可能有多个a满足条件（即a可以加上n的整数倍，只要在0到 $t^{}-$2t−1 内）。然而，由于 $t^{}$2t 远大于n（我们取 $t\approx lo\left(n\right)$t≈2log2​(n) ，所以每个b大约有 $t^{}/n$2t/n 个a满足条件。因此得到：

$K\approx t^{}=$K≈2tn2t​=n22t​

4. 量子傅里叶变换分析

由于我们对reg1进行了测量，所以reg2发生了坍缩，注意坍缩后的态依然是叠加态，是所有满足 $f(a,b)=Q$f(a,b)=Q 的$(a,b)$(a,b)对的叠加态。这个叠加态中包含了周期信息，因此现在我们需对reg2（大小为2t个量子比特）应用量子傅里叶变换以提取出周期信息。注意，寄存器2由两个寄存器（分别存储a和b）组成，因此我们分别对a和b的部分应用 $$QFT （即应用 $$QFT2t​ ，或者等价于对a部分应用 $$QFTt​ ，再对b部分应用 $$QFTt​ ，因为$$QFT是张量积的）。

对Reg2应用 $QF$QFT2t​ （即对整个2t个量子比特进行量子傅里叶变换）。 $QF$QFT2t​ 的作用是将时域/空域中的周期信号变换为频域中的尖峰：

$QF\mid a,b⟩={\sum }_{c=}^{t^{}-}{\sum }_{d=}^{t^{}-}{e}^{\pi i(ac+bd)/t^{}}\mid c,d⟩$QFT2t​∣a,b⟩=2t1​∑c=02t−1​∑d=02t−1​e2πi(ac+bd)/2t∣c,d⟩

因此，变换后的状态为：

$\mid ⟩={\sum }_{c=}^{t^{}-}{\sum }_{d=}^{t^{}-}{e}^{\pi i(ac+bd)/t^{}}\mid c,d⟩=\left[e^{\pi i(ac+bd)/t^{}}\right]\mid c,d⟩$∣ψ4​⟩=2tK​1​∑(a,b)∈S​∑c=02t−1​∑d=02t−1​e2πi(ac+bd)/2t∣c,d⟩=K​1​2t1​∑c,d​[∑(a,b)∈S​e2πi(ac+bd)/2t]∣c,d⟩

5. 寄存器2测量与概率分布

当我们测量reg2时，寄存器状态会坍塌到特定的(c,d)，由于reg2在应用量子傅里叶变换前具有周期性，因此此时我们测量reg2得到值大概率会出现在频域尖峰附近，坍缩后系统的态为：

$\mid =\left[e^{\pi i(ac+bd)/t^{}}\right]\mid c,d$∣ψ5​⟩m​=2tK​1​[∑(a,b)∈S​e2πi(ac+bd)/2t]∣c,d⟩m​

因此，我们需要计算内层求和：

$ac+bd=(m-kb)c+bd=mc+(d-kc)b\Rightarrow e^{\pi i(ac+bd)/t^{}}=e^{\pi i[mc+(d-kc\left)b\right]/t^{}}$ac+bd=(m−kb)c+bd=mc+(d−kc)b⇒∑(a,b)∈S​e2πi(ac+bd)/2t=∑(a,b)∈S​e2πi[mc+(d−kc)b]/2t

由于 $a,b$（a,b） 按照 $b=....t^{}-$b=0，1，2，....，2t−1 ，并且按此确定 $a$a ，也就确定了向量。因此我们将$a,b$（a,b）和 $b$b 都参数化为 $s$s 。即设 $b=s$b=s ，那么 $a=m-ks\left(modn\right)$a=m−ks( mod n) ，由此，我们就将向量$a,b$（a,b）转化成为关于 $s$s 的函数了。

由此，内层求和变化为：

${\sum }_{s=}^{K-}{e}^{\pi i[mc+(d-kc\left)s\right]/t^{}}=e^{\pi mci/t^{}}{\sum }_{s=}^{K-}{e}^{\pi i(d-kc)s/t^{}}$∑s=0K−1​e2πi[mc+(d−kc)s]/2t=e2πmci/2t∑s=0K−1​e2πi(d−kc)s/2t

设 $r=e^{\pi i(d-kc)/t^{}}$r=e2πi(d−kc)/2t ,则求和部分:

$S={\sum }_{s=}^{K-}{r}^s=,r\ne$S=∑s=0K−1​rs=r−1rK−1​,r=1

当 $r=$r=1 时即 $e^{\pi i(d-kc)/t^{}}=$e2πi(d−kc)/2t=1 ，根据欧拉公式 $e^{i\theta }=\cos \theta +i\sin \theta$eiθ=cosθ+isinθ 得知：

$\cos \left(\pi \right(d-kc\left)/t^{}\right)+i\sin \left(\pi \right(d-kc\left)/t^{}\right)=$cos(2π(d−kc)/2t)+isin(2π(d−kc)/2t)=1

也就是说当 $(d-kc)/t^{}$(d−kc)/2t 为整数时，所有的值刚好在波峰上相长干涉，因此累加后得到 $S=K$S=K ，综合一下：

S={K=22t/nr−1rK−1​​r=1r=1​

综上，令$\gamma =d-kc$γ=d−kc，则最后得到有效测量值（c，d）的概率分布为（计算过程参考RSA这篇文章）：

P(∣c,d⟩)={K22t​1​=22tn​K22t​1​∣r−1rK−1​∣2=22tn​⋅sin2θ/2sin2Kθ/2​​r=1r=1,θ=2πγ/2t​

注： $\mid {\mid }^{}=\mid (e^{\pi iK\gamma }-)/(e^{\pi i\gamma }-){\mid }^{}=({)}^{}=$∣r−1rK−1​∣2=∣(e2πiKγ−1)/(e2πiγ−1)∣2=(cosθ+isinθ−1cosKθ+isinKθ−1​)2=sin2(θ/2)sin2(Kθ/2)​

[培训]Windows内核深度攻防：从Hook技术到Rootkit实战！