从Bottom出发达到的一定是最小不动点

从Top出发到达的一定是最大不动点

对于Transfer Function的单调性，我们需要回到之前的章节

以这个为例子，在课程中笔者认为该例子过于晦涩难懂，仅仅因为 genB固定 KillB固定就证明该函数是单调的。但实际上我们可以通过一个不严谨的思想来理解这个Transfer Function是单调的，我们考虑将该函数类比为 普通的一次函数

y = const1 + x - const2

其中

y = OUT[B]

const1 = genb

x = IN[B]

const2 = killB

通过如上的类似仿射变换的思想可以帮助我们理解Transfer Funcion的单调性。

合理严格的证明如下

这里的证明思路还是阐述一下方便理解。

经过如上的证明我们能够将数据分析的问题转化到格上，且能够通过获取lfp和gfp 得到Best Fixed Point，也能够证明这些问题是一定有解的。

现在我们需要讨论什么时候我们能够抵达不动点。为了解决这个问题我们需要引入格的高度这个概念。

格的高度就是从 Top 到 Buttom最长的一条路径就是 格的高度

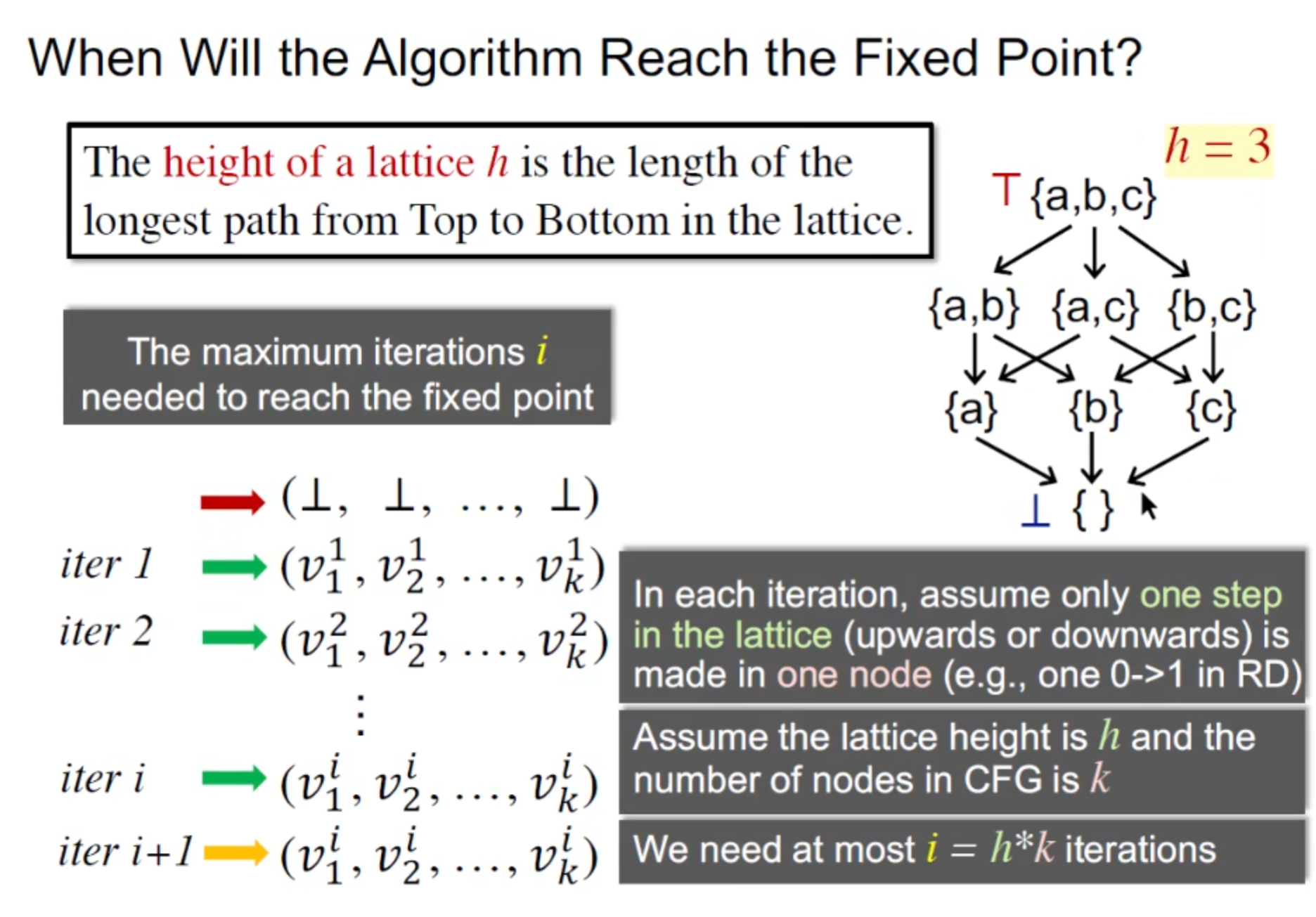
最坏的迭代次数就是 格高度 * 节点个数 该次数是悲观上界 辅佐以下图理解，不过我们需要申明几个前提

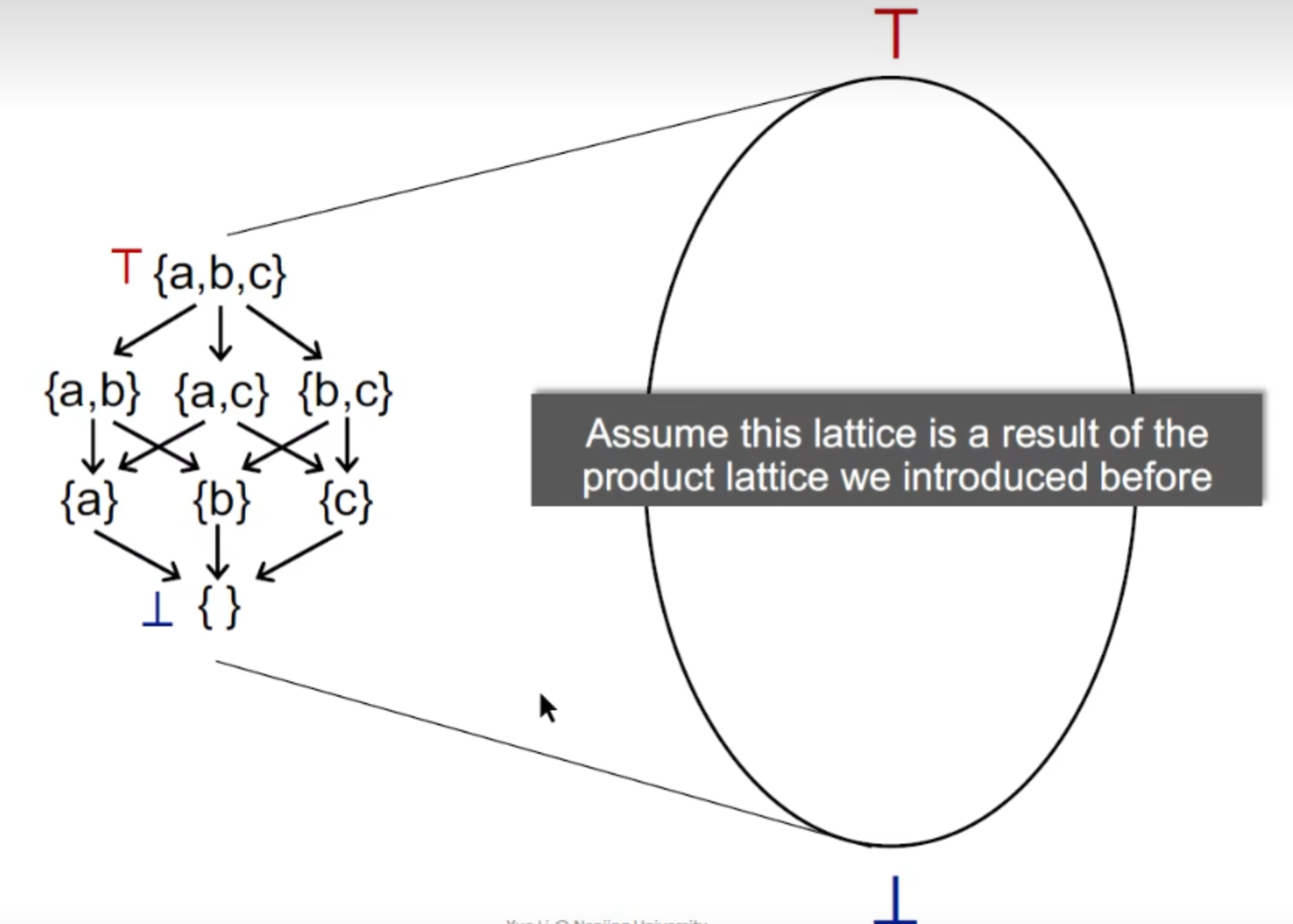
我们可以考虑把一个PL的 抽象的Lattice 的 Product Lattice看成一个新的Lattice

对于May 我们通常是从 Bottom 出发从一个unsafe result到 safe result的过程

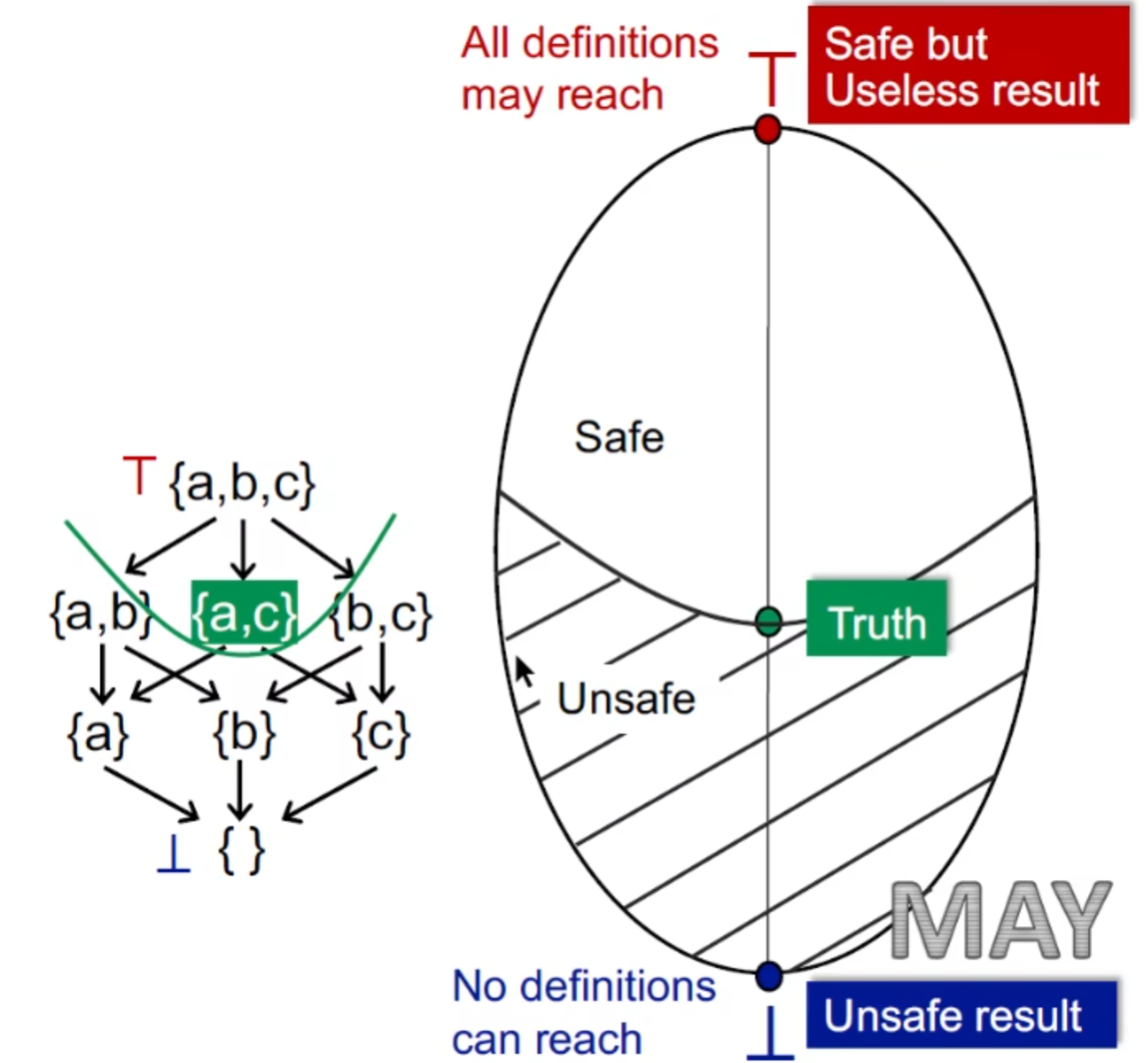
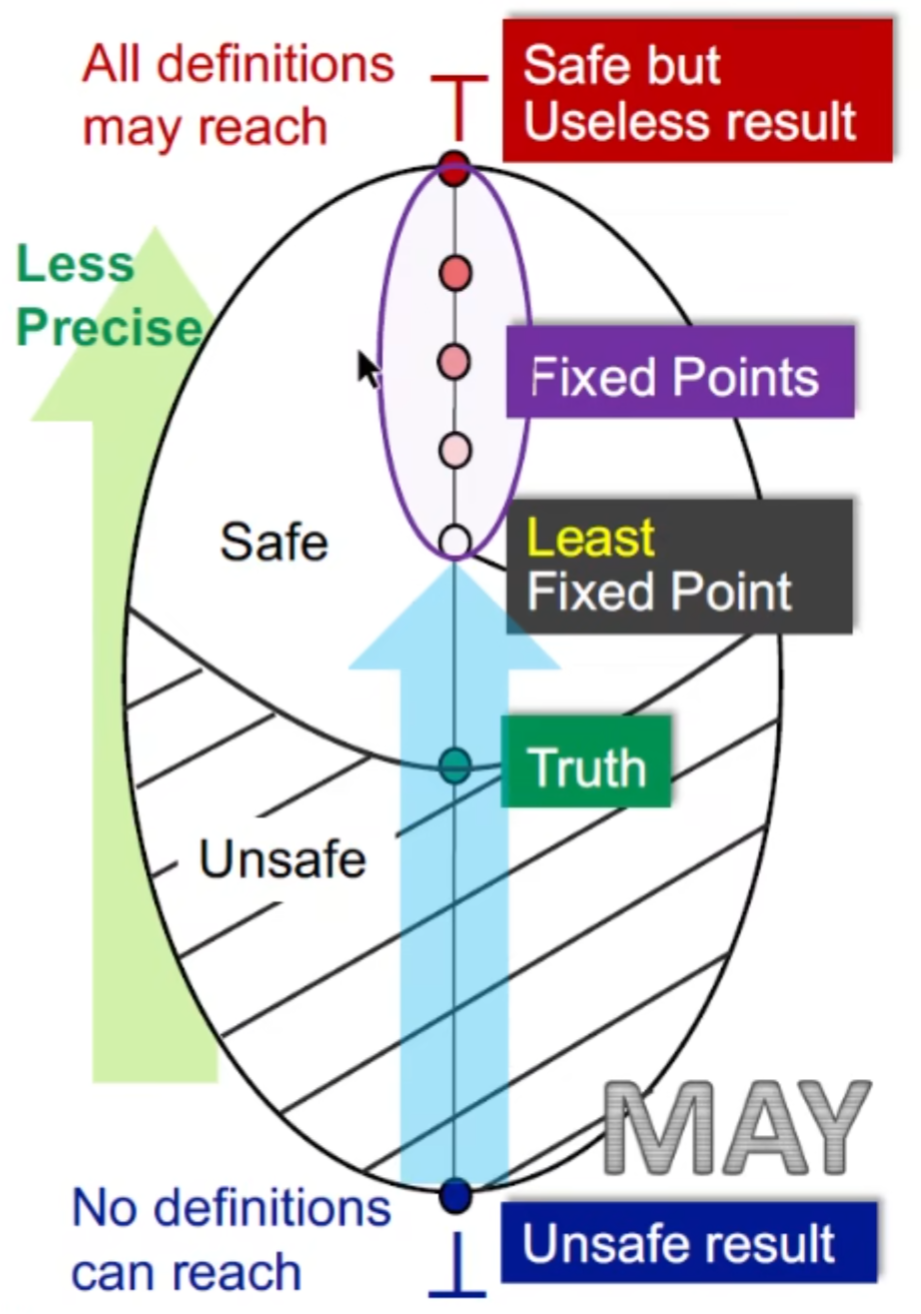
结合这张图我们用 Reach Def 举例子

在Reaching Definitions问题中，我们在Entry块给所有变量一个undefined定义。在格中：

这里我们做一个类比理解

想象你问："明天会下雨吗？"

回答

对应

评价

"不知道"（啥都没说）

⊥ (Bottom)

❌ 不靠谱（可能错过重要信息）

"有30%概率下雨"

不动点

✅ 靠谱且有用

"明天可能下雨，可能晴天，可能下雪，可能刮风，可能地震，可能外星人入侵..."

⊤ (Top)

✅ 靠谱（肯定不会错）❌ 但完全没用

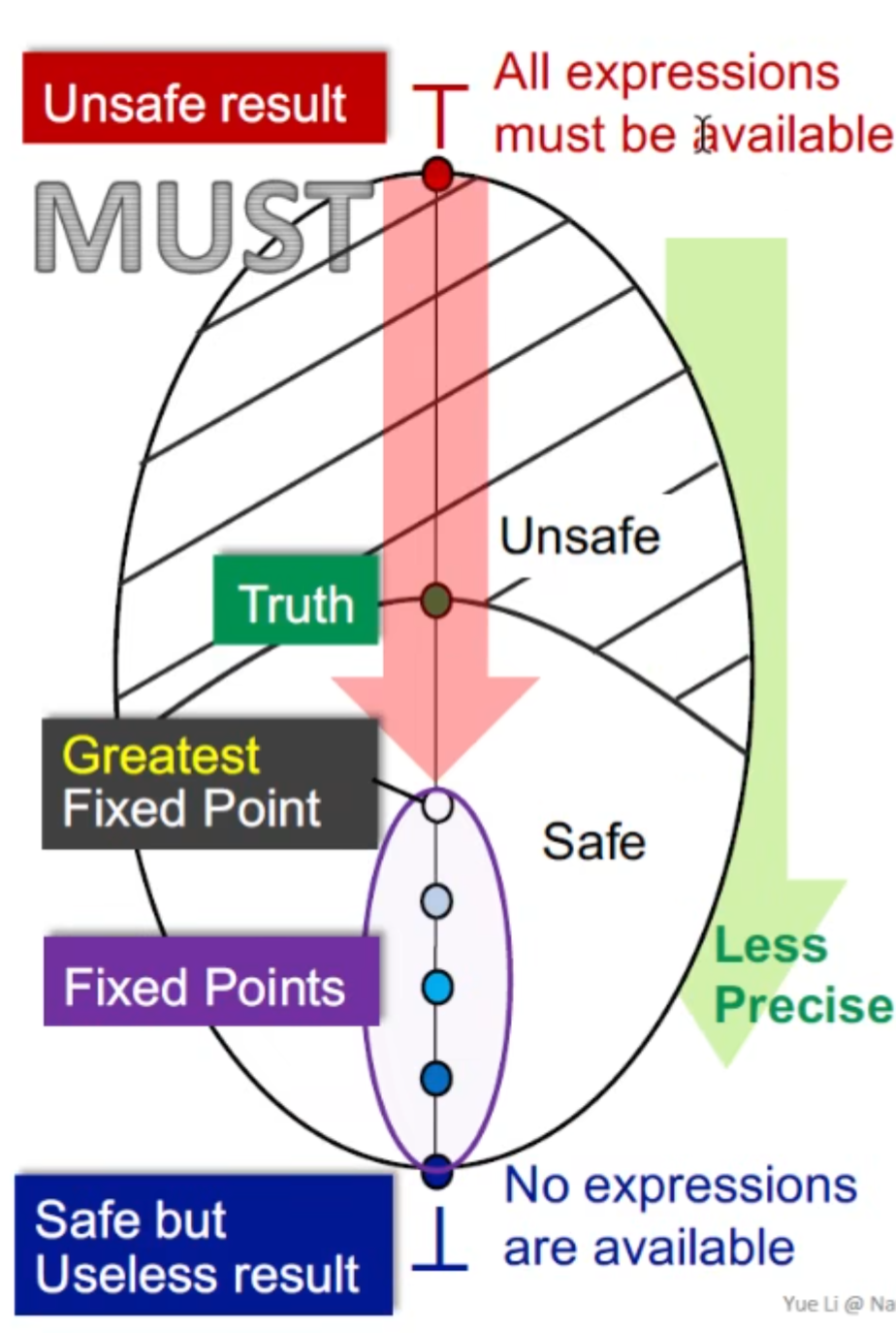
Available Expressions分析是Must分析，目标是找出在某个程序点肯定被计算过且还有效的表达式（用于优化，如公共子表达式消除）。

格的结构

Top (⊤) = 所有表达式的全集

Bottom (⊥) = ∅ (空集)

我们给出该图进行回顾总结

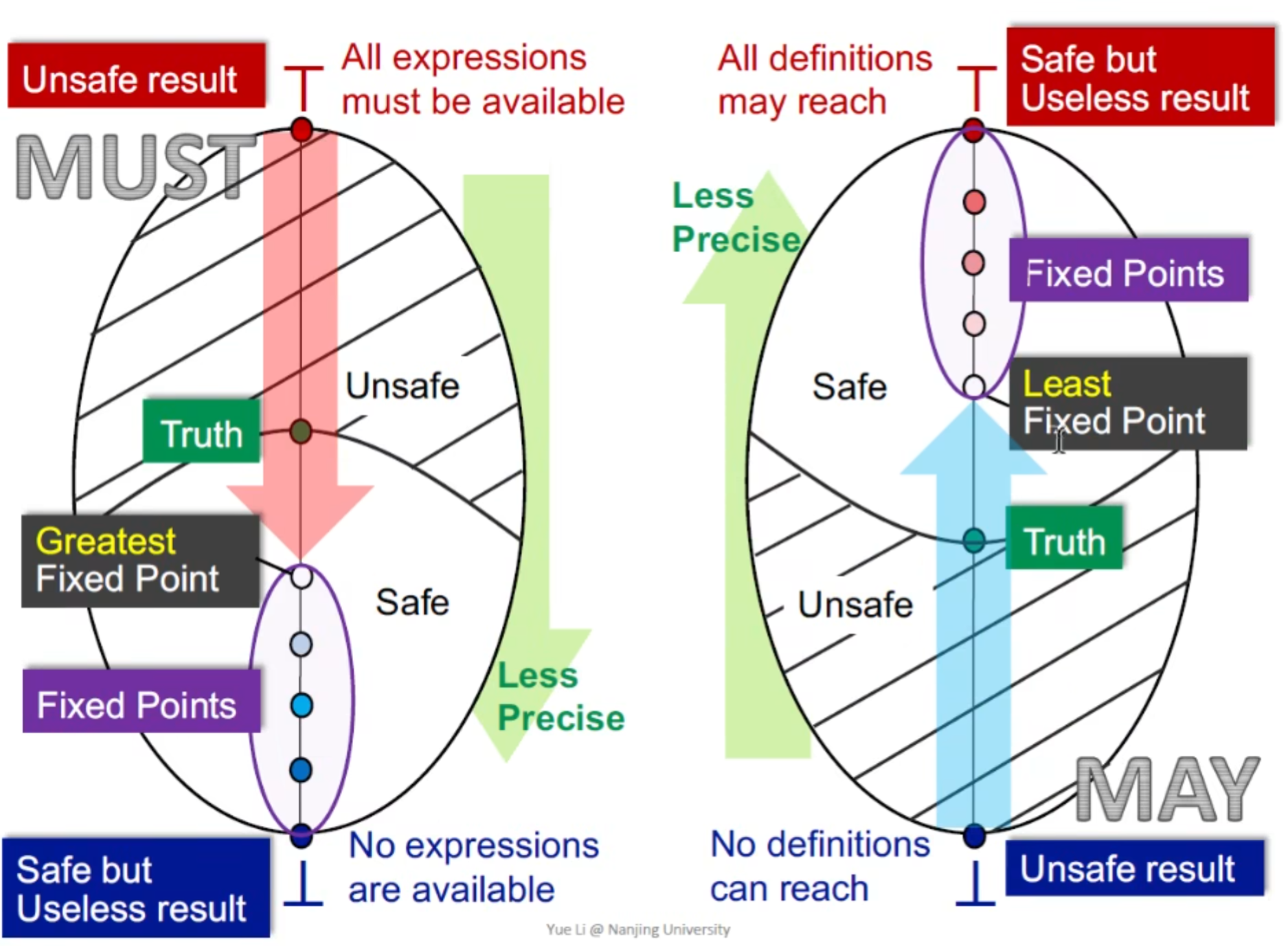
Definitions问题

视角

问题

分析类型

May

"哪些定值可能到达？"

May Reaching Defs

Must

"哪些定值一定到达？"

Must Reaching Defs

Expressions问题

视角

问题

分析类型

传播安全知识、拓宽行业人脉——看雪讲师团队等你加入！