我们开启抓包进入APP，发现第一个请求便是指纹数据。数据包如下：

查看 Content-Type 发现使用的二进制格式发送的数据包，因此我们排除这是 Base64 编码的数据包。

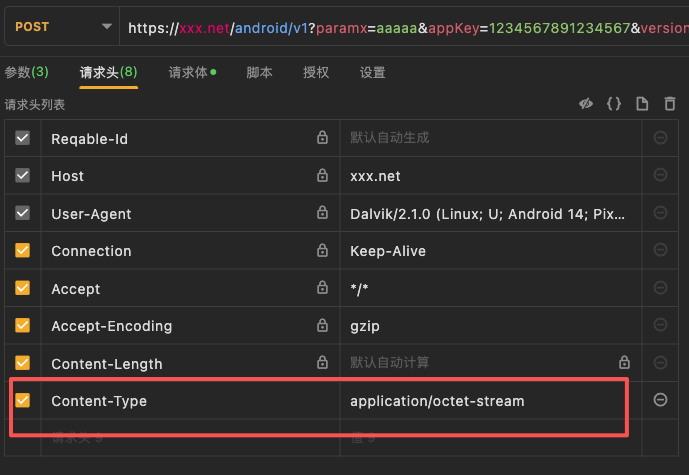
现在我们需要知道，数据包是从哪里发出的。我们 HOOK 一下 RegisterNatives，看看发包前加载了哪些 SO 以及注册了哪些函数。

观察得知在发包前 SO 注册了上图这个函数，我们 HOOK 一下这个函数看看调用情况。

这里看到一共调用了三百多次，这是典型的传入不同编号走不同处理分支的分发函数，各大厂的算法与设备信息收集都是这样设计的。因此，我们可以大胆下判断，发包的请求就藏在这三百多个调用中。那么我们怎么确定是哪个编号发出的请求呢？我们可以 HOOK 一下 memcpy 函数，因为在 Native 层要进行数据传递通过 memcpy 来复制数据十分便捷高效，而数据包就极有可能在 memcpy 中被复制过。这里插播一个知识点：为什么各大厂商都知道 memcpy 可能是是暴露数据的库函数，为什么还要调用它，而不自行实现？因为 libc 中的 memcpy 使用汇编实现，同时针对不同的 cpu 架构会使用特定的高级指令来加速数据的拷贝。我们可以查看 AOSP 中的 common/arch/arm64/lib/memcpy.S 文件源码来验证：

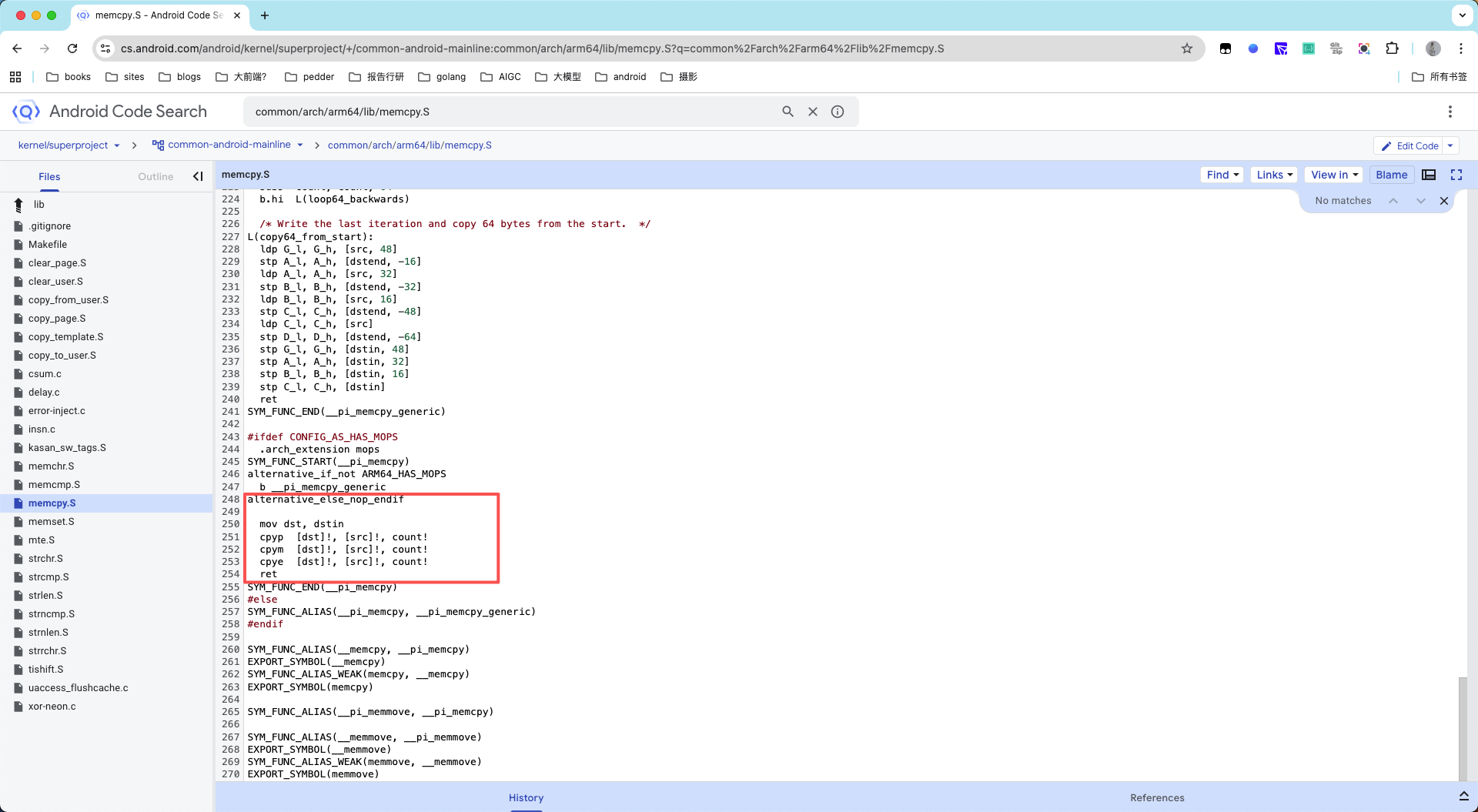
可以看到这里判断了是否支持 MOPS ，如果支持则使用特定指令完成拷贝。而且部分编译器在编译期间会将 memcpy 替换为 memcpy_chk 函数，memcpy_chk 是增加了 src 缓冲区长度校验的版本，防止缓冲区溢出从而导致程序崩溃。这也相当于为程序的健壮性做了兜底保证。当然，如果厂商想硬实现 memcpy 也是可以的。但是这仍不能避免被我们分析，因为最终 APP 要运行在我们的设备上，而设备是我们能完全控制的。因此，在性能与实现复杂度的双重考量下，大部分厂商仍选择使用库函数的 memcpy。下面，我们回到正题。我们 HOOK memcpy 的同时将函数的调用编号也打印出来，观察目标数据包前后的函数编号，以此来确定是在哪个编号中发出的数据包。

从上图中我们可以看出在目标数据包前后，有两个编号：83、12。我们怎么判定是在哪个编号中发出的请求？可以分别搜索一下这两个编号，看看哪个编号是第一次被传入的，如果有编号是第一次被传入的那么大概率便是这个编号发出的数据包。经过搜索发现编号 83 出现了两次，而 12 只出现了一次，那么我们可以初步判定编号 12 为发包编号。那么我们怎么判定这就是最终的发包编号？我们可以在编号 12 被传入时，将进程暂停，如果暂停了仍然发包出去了，那么证明 12 不是最终的发包编号，反之则实锤这是发包编号。下面我们验证：

在编号 12 被传入时我们暂停进程 5 秒，观察抓包发现并没有请求发出，那么至此我们可以确定数据包就是在编号为 12 的函数调用中发出。知道了发包的位置，接下来我们看看包数据是怎么组装加密的。

在我们HOOK RegisterNatives 时得到了分发函数的偏移 0x82f14。现在我们进入SO中看看这个函数。

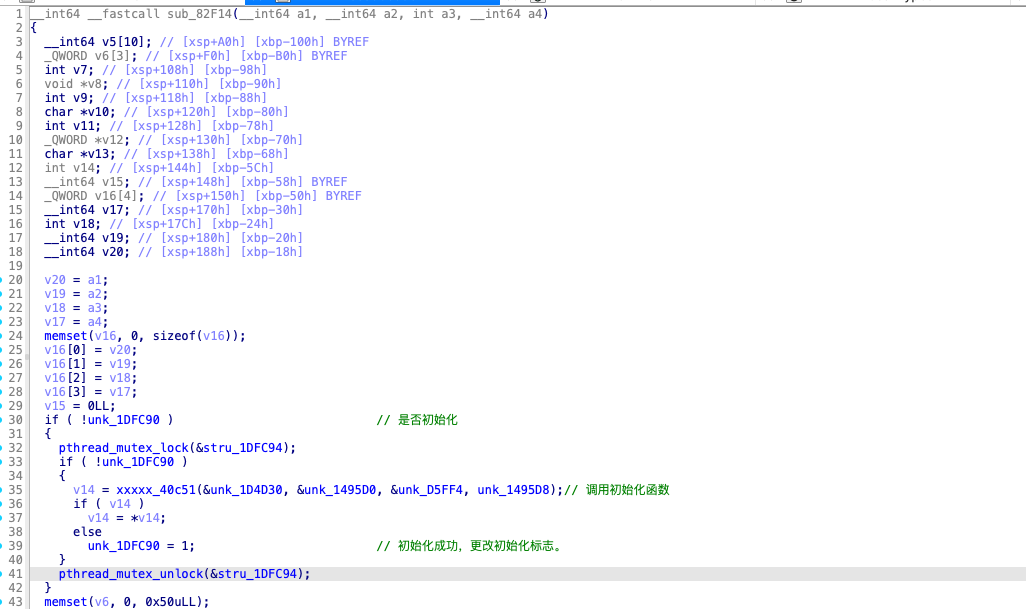
这个函数只是做了些初始化引导工作，我稍微跟了下初始化函数发现是有 OLLVM 混淆与 VMP 防护的。

这种情况下如果我们不深究其虚拟机实现的话，可以使用 trace 方案拿到执行指令流展开算法的分析。这里我用自己写的 trace 跟踪了编号 12 函数调用时的指令流，最终得到一个 8.3G，8000W 行的指令流文件。

现在我们已知加密密文如下：

既然我们得到了完整的指令流文件，那么密文数据一定会在某条指令中出现。因此，我们可以在文件中搜索对应的字节来找到密文生成的位置。

我以四个字节为一组尝试在文件中搜索，直至搜索到 33-36 字节时，也就是 0751AC3F，才第一次在文件中搜索到对应数据。

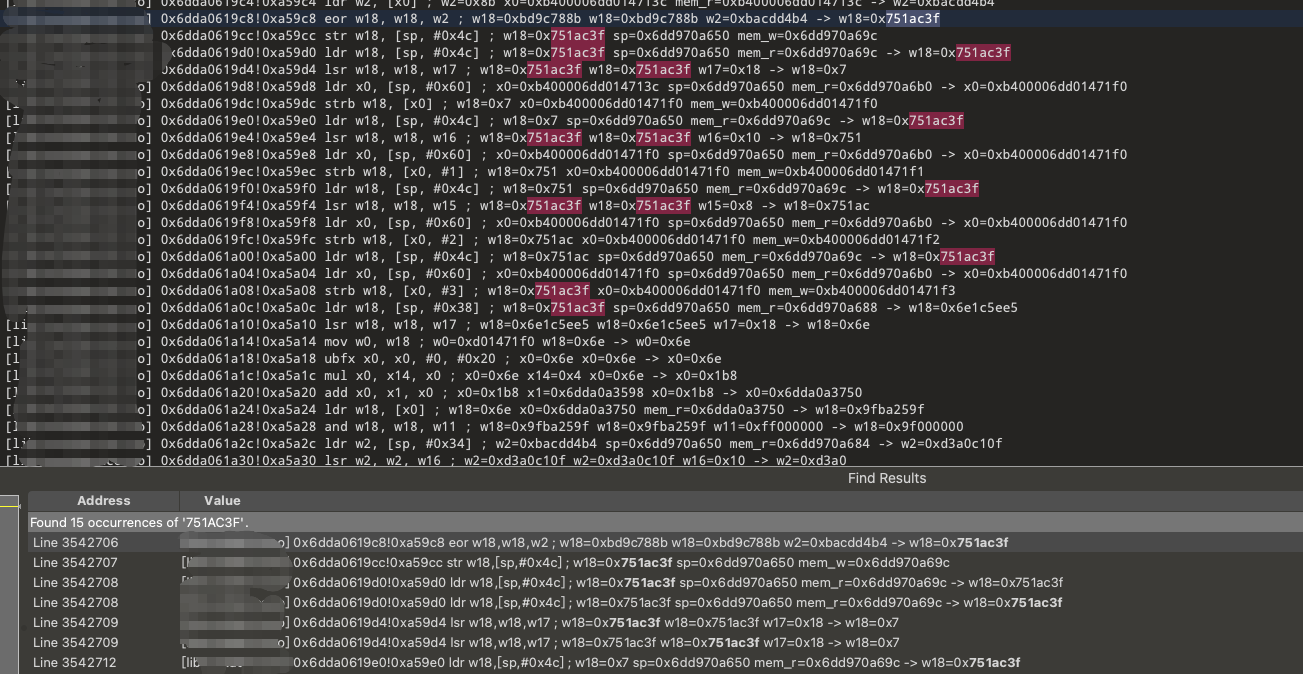
我们可以看到，这组数据第一次生成的位置在 0xa59c8 ，因此我们在IDA中跳转到目标地址查看伪代码看其是如何生成的。

跳转到 0xa59c8 后我们看到这个函数，函数中有大量的查表与异或操作，因此我们可以判断这是一个加密函数。既然是加密函数，那么我们就要识别这是个什么加密算法。我们可以看看这四个表的数据分别是什么，以此来判断这是什么加密算法。

我们可以看到表1与表2分别有大量的 63 7C 77 99 等字节出现，这些字节一般会出现在 AES 加密算法中的 S 盒中，因此我们初步判断这是个类 AES 算法。我们再观察下加密函数发现，a1 一进来便与 a3 进行了异或。而我们通过伪代码可知 a1 是个长度为 16 的字节数组，a3 是个长度为 4 的字节数组。将 a1 中的数据以四个字节为一组，通过 << 位操作组成一个 32 位的数据以对应 a3 的数据格式，随后与 a3 进行异或。我们再观察下函数的结尾部分，对 a2 中的每个元素进行赋值，赋值长度为 16，并且每个赋值语句的最后一步都是为 v19 进行异或，而 v19 是由 a3 赋值而来。因此我们得出如下结论：

将输入数据 a1 经过加密得到输出数据 a2，每一轮循环中都有与 a3 异或的步骤。每轮异或的字节长度为 16，并且输入输出数据长度也均为 16 。

我们回忆下 AES 128 算法实现：

1byte = 8bit 16byte * 8 = 128bit

输入明文 128 bit，输出密文 128 bit。加密开始时输入明文与扩展密钥进行异或，随后进行 10 轮加密，最后一轮的最后一步是与扩展密钥进行异或得到最终密文。现在我们将 AES 128 与我们得到的结论进行对比发现三个相似点：

并且结合表数据判断，我们可以确定这是个魔改 AES 128 查表实现。查表实现是标准实现的性能优化版，节省列混淆的计算过程达到提升性能的目的。并且在逆向中不易被还原。

现在我们确定了加密算法为 AES 128，那么我们就可以根据 AES 的实现步骤来找到密钥。现在我们已知的信息有：

我们知道 aes 最后一步加密为 state ^ key = ciphertext。因此，我们可以在指令流中找到最后一步密文生成的位置，看看是哪些数据与 state 异或后得到了密文，与 state 异或的便是密钥。

我们可以看到

这行指令便是密文最终生成的位置。我们将其还原成伪 C 代码：state = state ^ key 也就是说左边的 w18 是 state，右边的 w2 为密钥。至此我们就得到了最后一轮的第一组密钥：0xbacdd4b4。

那么我们怎么得到最后一轮的全部密钥呢？我们可以以四字节为一组依次向后搜索密文生成的位置，将所有的被异或寄存器拼接起来便是最后一轮的密钥。搜索后得到如下四条指令：

将被异或寄存器的值拼接起来，我们得到了最后一轮的密钥：

ba cd d4 b4 ad 65 51 1d 3c d4 b0 f6 43 26 b3 a4

现在我们验证一下我们的密钥是不是正确的。根据 AES 的密钥扩展算法可知，我们只需要得到任意一轮中的密钥，就能逆推出初始密钥。这里我们使用 Stack 提供的实现来逆推出初始密钥。

我们看到 Stack 逆推出了每一轮的密钥，现在我们以四个字节为一组在指令流中搜索密钥。如果能搜到则证明我们的密钥没有问题。

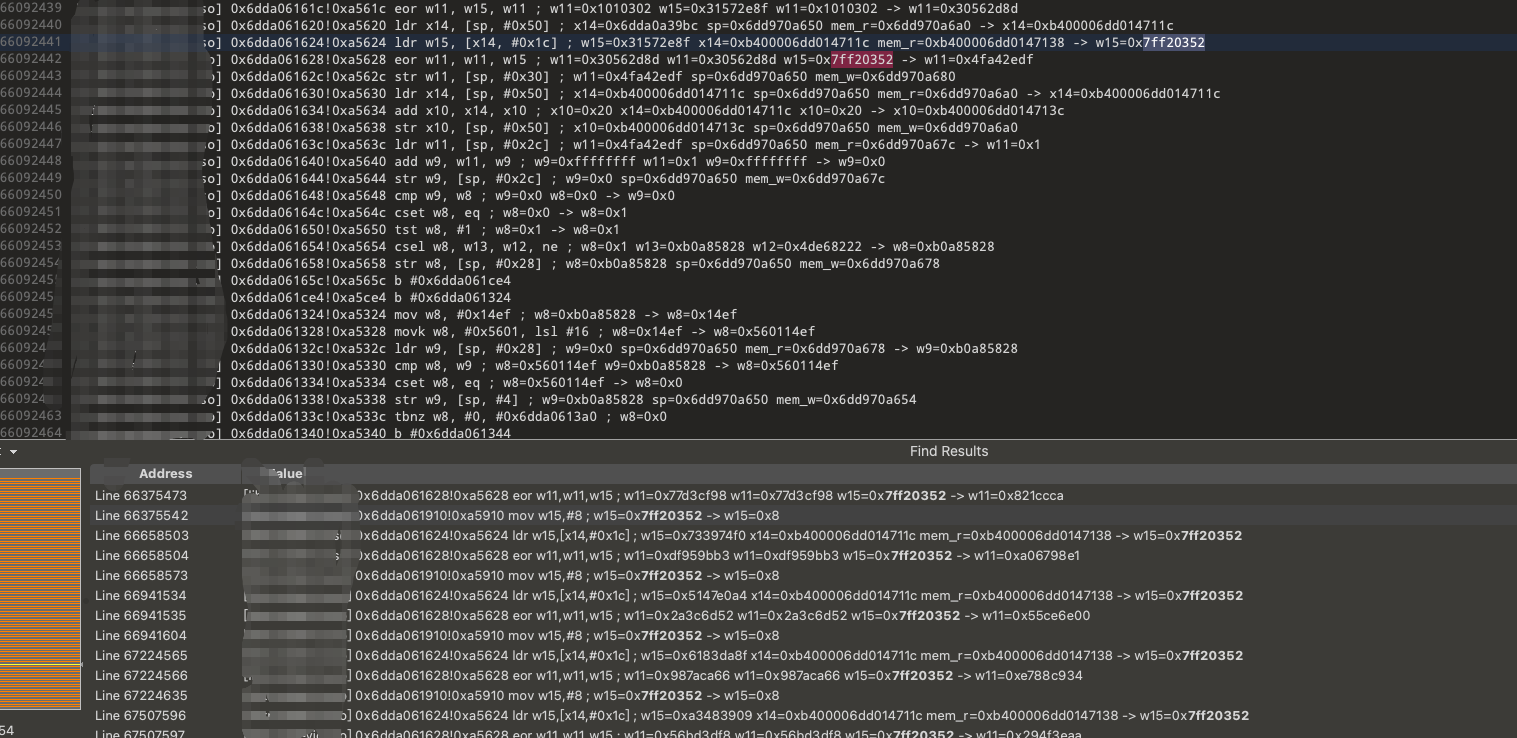
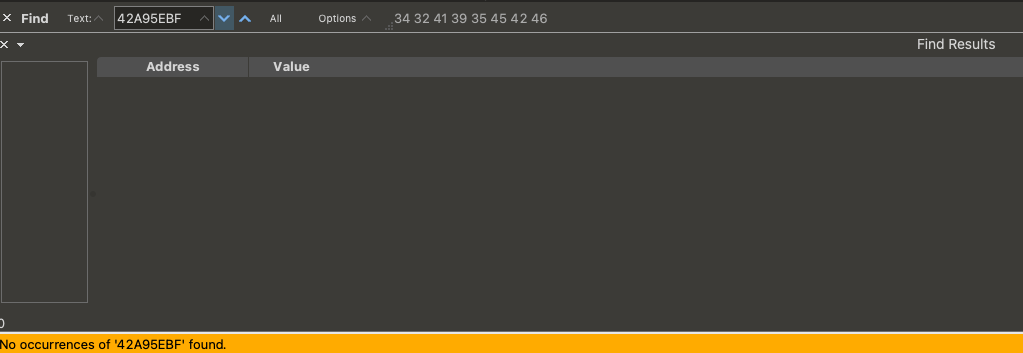
我们可以看到 K09 的最后四个字节能搜索到，而初始密钥 K00 的最后四个字节却搜索不到。因此，我们可以断定厂商魔改了密钥扩展算法。接下来，我们还原密钥扩展算法。

在搜索 7FF20352 时发现一共有 954 个结果，而第一个结果便是 7FF20352 最初生成的位置。

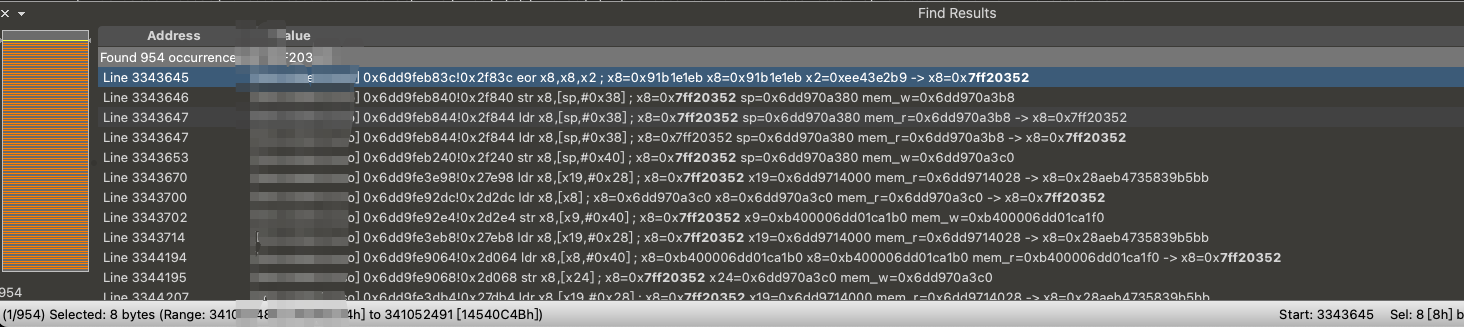
因此我搜索了 0x2f83c 地址执行的所有指令，发现最后一轮与 K09 的密钥均在这条指令中出现：

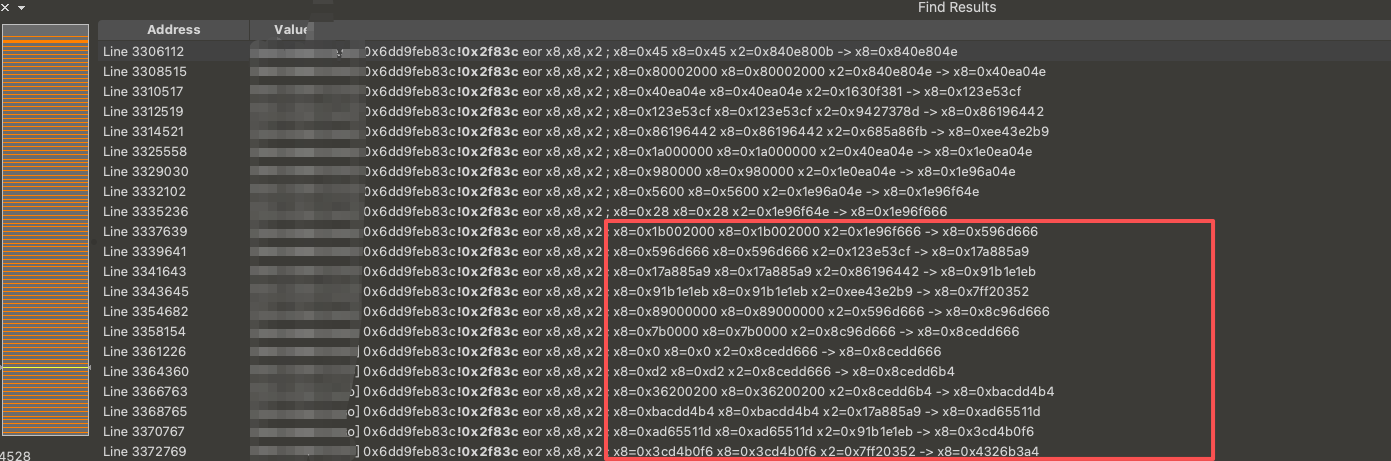
那么我们可以判断，这条指令是密钥扩展算法中的最后一条指令。那是不是意味着我们在 IDA 中跳转到这个地址，就能看到魔改后的密钥扩展算法？我们跳转到目标地址看看：

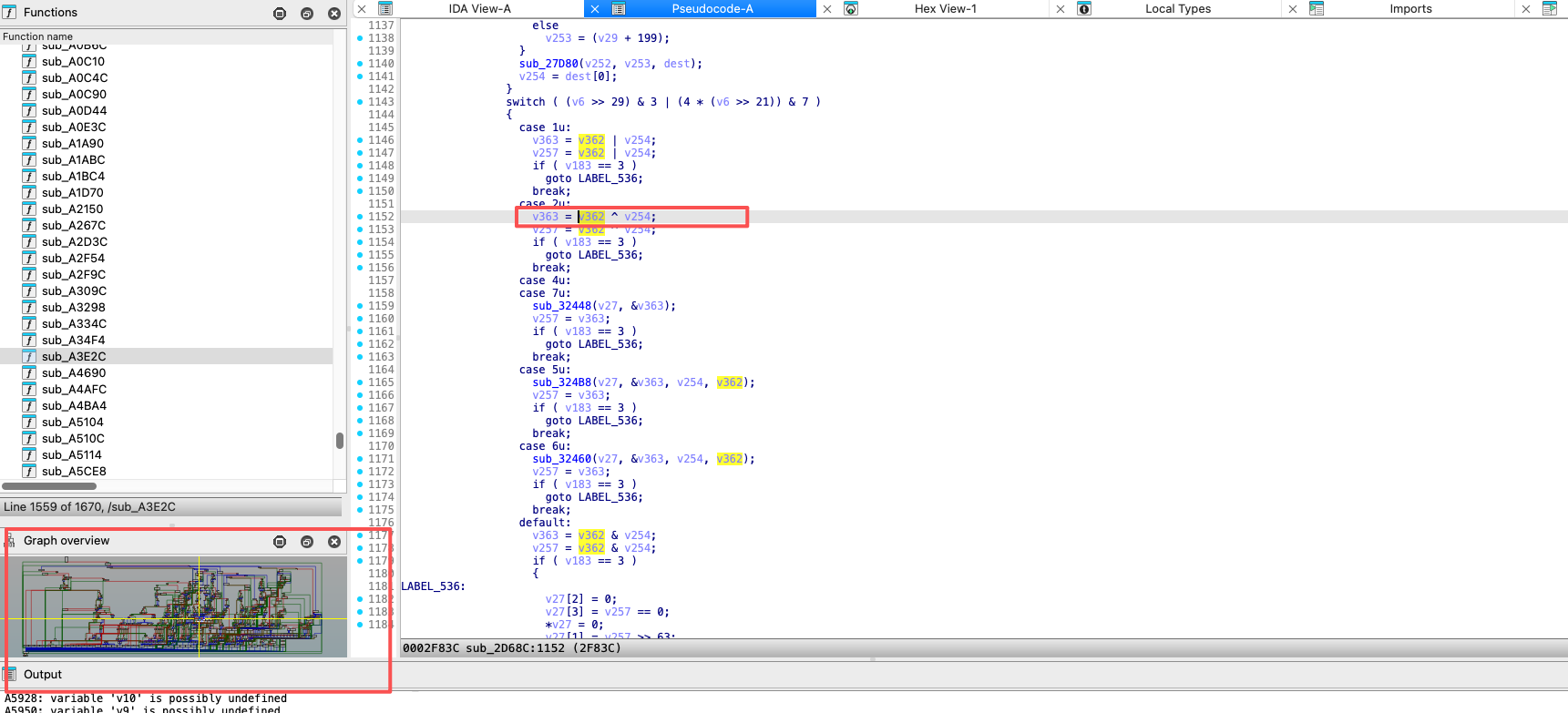
跳转到 0x2f83c 后我稍微看了下这个有 3000 多行的函数，这貌似是个 VM 的分发器。并且通过左下角的调用链可以看到这是个经过了超高强度的混淆函数，而且没有任何与密钥扩展算法相关的信息。因此，我们只能回到汇编指令流中来分析密钥扩展算法。

在 0x2f83c 这条指令搜索结果中的最上面，我们有了意外发现：

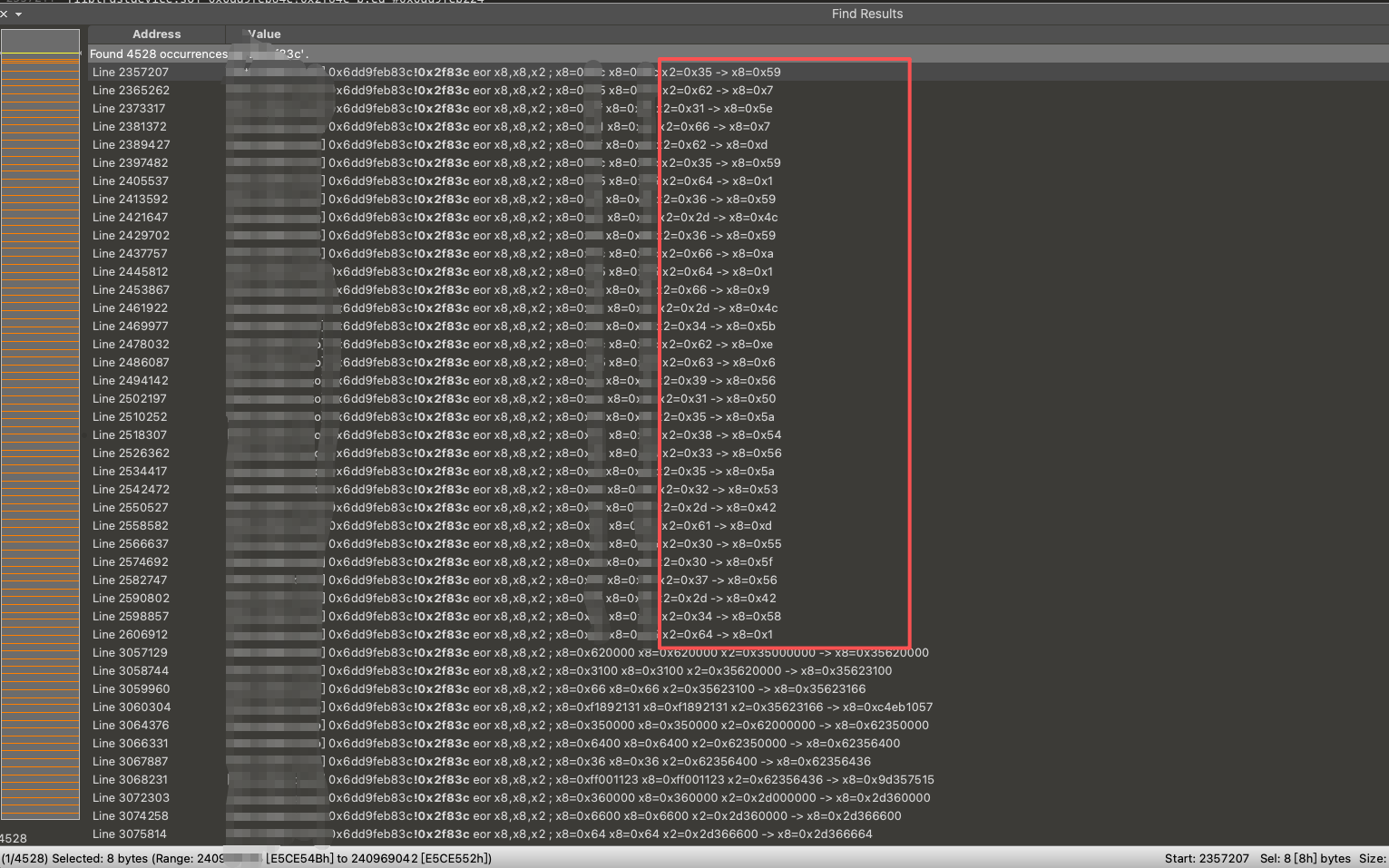
我们看到标红区域的 X8 结果便是我们发送的数据包开头 32 个字节。并且这些结果都是 X8 与 X2 异或得来的结果，异或之前 X8 的值是一串固定的常量，因为异或之前的 X8 与厂商信息有关，所以我将其码掉了。现在，我们思考为什么要将这 32 个字节与固定常量异或后发送给服务端。是不是因为这是密钥？如果我们顺着这个逻辑思考下去便可以推导出：与固定常量异或是为了隐藏初始密钥，防止密钥暴露在请求数据包中。而为什么要将它发送给服务端呢？因为服务端拿不到初始密钥便不能对数据包进行解密。

事实上，动态密钥上报是非常常见的设计。如果厂商使用一个固定的密钥来对数据进行加密，那么攻击者只用破解成功一次便可以拿这串密钥去解密这个厂商旗下所有的 APP。而使用动态密钥迫使攻击者每碰见一个 APP 就必须得去找到固定常量才能解密密钥，因此这相当于增加了攻击成本。这是一个非常好的对抗策略。

如果我们不能保证应用 100% 不被破解，那么至少我们可以增加攻击者的攻击成本以达到让攻击者停止攻击的目的。

好了，我们言归正传。现在我们思考，为什么是 32 个字节呢？在 AES 128 加密中密钥只占 16 个字节，如果密钥只占 16 个字节那么剩下的 16 个字节是什么呢？我们不妨回顾下 AES 的加密模式有哪些？常见的有两种：ECB、CBC。ECB 与 CBC 模式的唯一区别便是：ECB 没有 IV（初始向量）参与运算，而 CBC 则必须有 IV 参与运算。而 IV 在 AES 的加密中也是 16 个字节，那么我们就可以初步判断这 32 个字节是 KEY + IV。那么我们怎么验证？在 CBC 加密模式中，CBC 将待加密的明文切割成一组组 16 字节大小的数据集，在将第一组明文输入进 AES 加密之前，先将明文与 IV 逐字节进行异或，再输入 AES 中加密。而后每一组的明文数据都与上一组的密文数据进行异或后再输入进 AES 加密。也就是从第二组开始 IV 便是上一组 AES 加密后的密文。好了，现在我们搞清楚什么是 CBC 加密模式后，我们验证一下，看不看是不是真的如我们所说使用 CBC 模式进行加密。

首先我们先整理出来密钥与IV：

密钥：35 62 31 66 62 35 64 36 2d 36 66 64 66 2d 34 62

IV： 63 39 31 35 38 33 35 32 2d 61 30 30 37 2d 34 64

我们还是看 0x2f83c 这条指令：

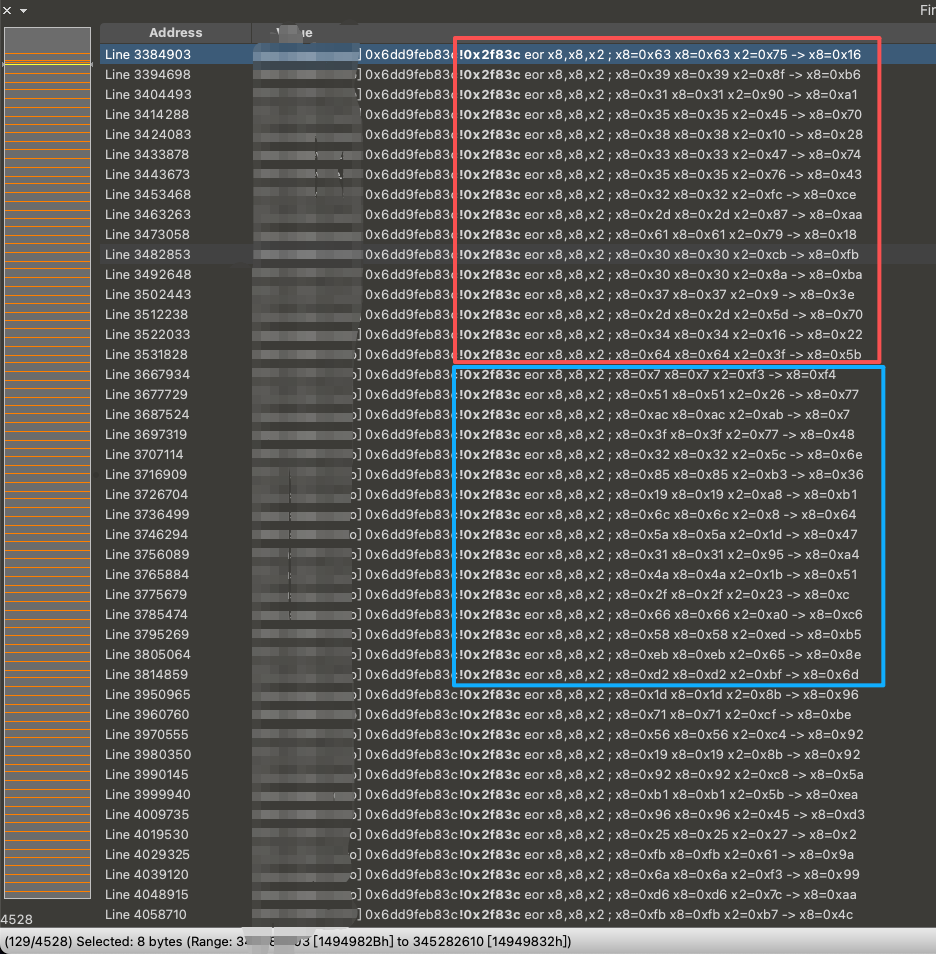
我们可以看到红色方框内 X8 异或之前的值便是我们的 IV，而蓝色方框内 X8 异或之前的值便是我们的第一组加密后的密文。符合我们所说的 CBC 从第二组开始将上一组的加密密文作为 IV 来与明文异或。至此我们确定了加密模式使用的是 CBC 并且我们找到的 IV 是正确的。现在我们需要知道我们的密钥是不是正确的。

我们回到这张图：

往上滚动到第一次出现四字节异或的位置：

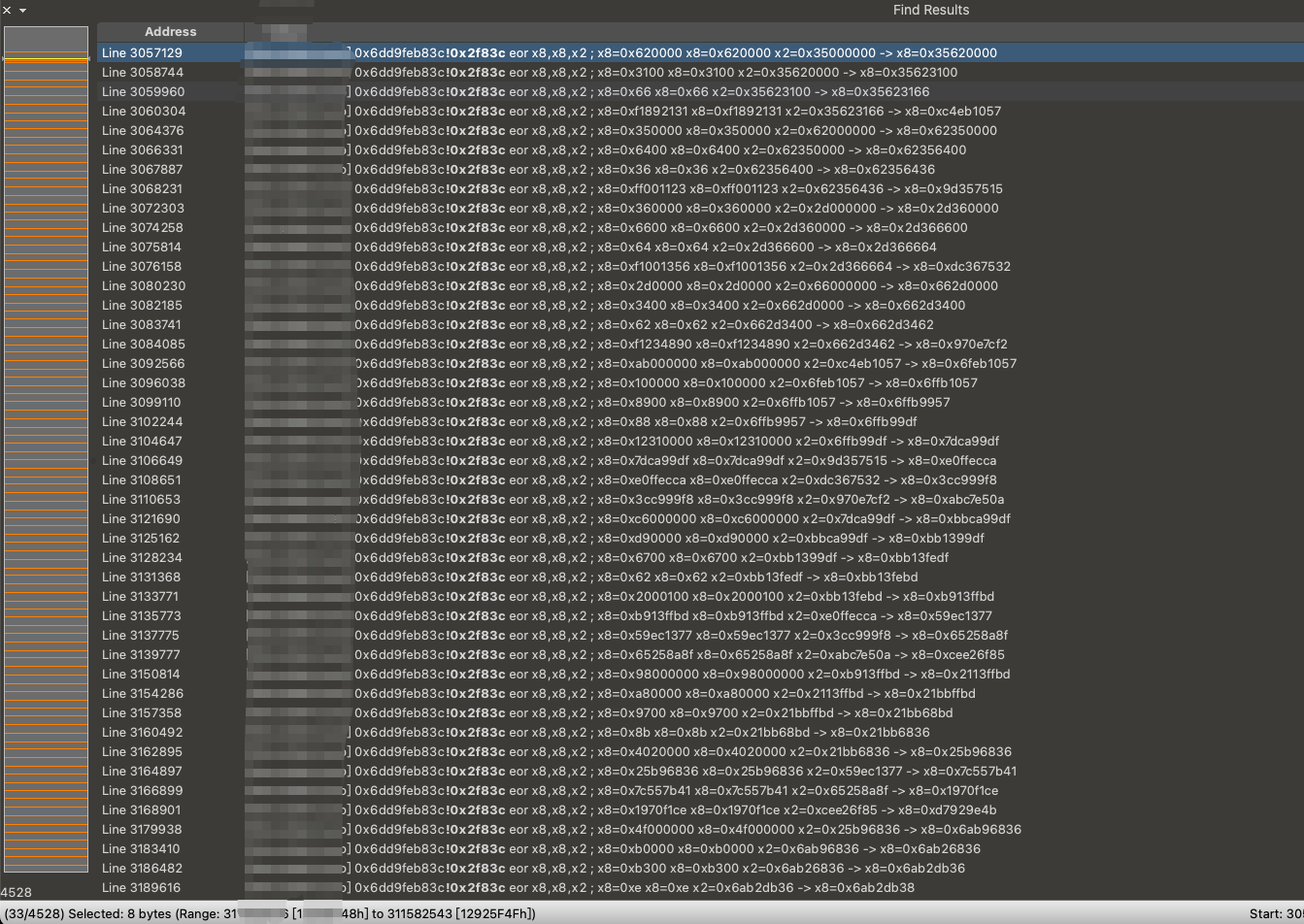
我们看到开头三条指令将我们的密钥前四个字节加载了出来，而后将密钥前四个字节与 0xf1892131 异或后得到 0xc4eb1057 。现在我们假设 0xc4eb1057 便是我们第一轮的第一组密钥，如果我们能在加密函数开头部分找到 0xc4eb1057 这个四字节与 a1 异或了，那么便证明这是第一轮的密钥。现在我们回到加密函数的开头指令流部分：

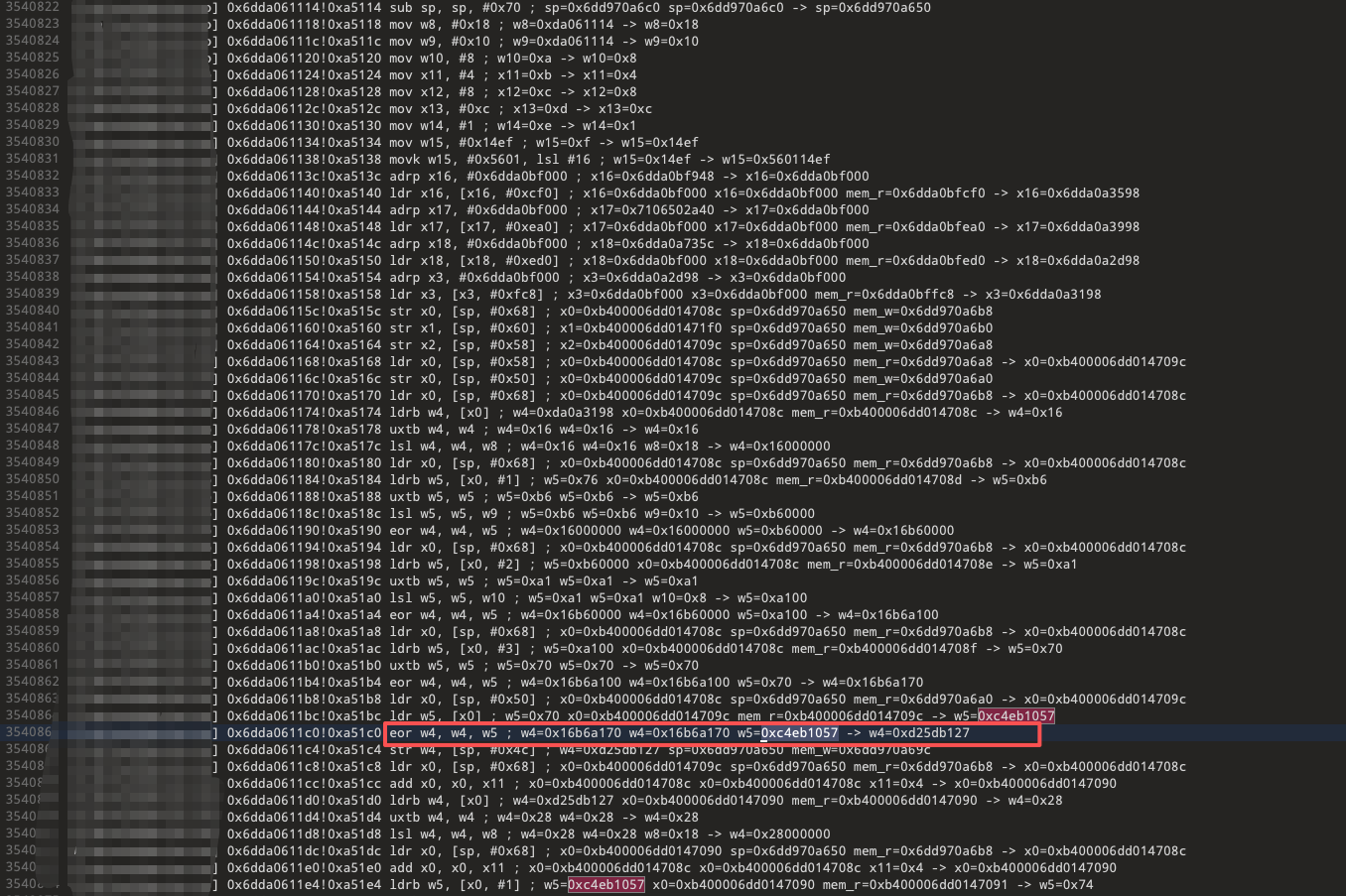
我们可以看到从函数地址 0xa5114 开始部分不到 50 行便找到了我们假设的密钥与明文进行了异或，并且我们可以看到 0x16b6a170 正是我们的初始 IV 与明文异或后的中间明文。

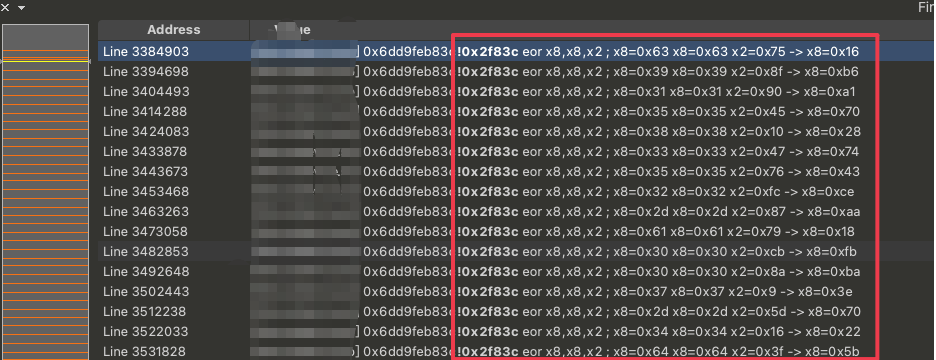
至此我们可以确定我们的密钥是正确的。现在我们拿到了正确的初始密钥就可以开始还原厂商魔改的密钥扩展算法。

再回到这张图：

我们发现第一轮第一组密钥是通过初始密钥 0x35623166 与 0xf1892131 异或得到的，因此我需要知道 0xf1892131 是如何而来的。我们还是在指令流中搜索这串数据：

我们可以看到这串数据通过一条位或指令得到。如果按照正常的还原流程我们还需要弄清除 X9 与 X8 的值是怎么来的，但是由于经过 VMP 加持的指令流变得非常之长，如果我们要在文章中展开怎么追溯 0xf1892131 生成位置的话，那么整个文章的结构与篇幅都将变得冗长、混乱不可读。因此，我在这里直接将与初始密钥异或的常量表给贴出来了。并且因为它是固定不变的，所以也不影响我们后续的阅读体验。

现在我们可以整理出与初始密钥异或后的 K00 轮密钥：

c4 eb 10 57 9d 35 75 15 dc 36 75 32 97 0e 7c f2

得到 K00 轮密钥之后我们需要知道 K01 轮密钥是怎么生成的，我们只要搞清楚 K01轮密钥的生成规则，就能按照相同的规则扩展出其余轮的所有密钥。

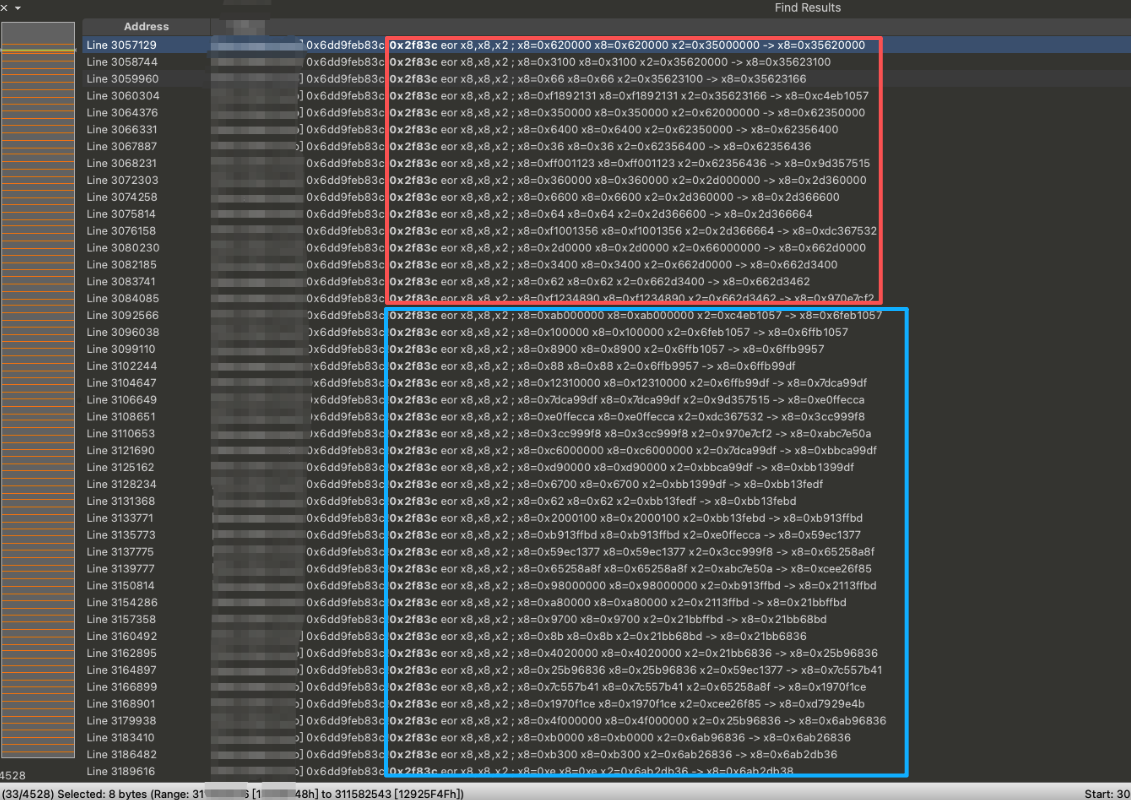通过这张图可以看到红色方框内标志着 K00 轮密钥生成的结束，蓝色方框内标志着 K01 轮密钥生成的开始。通过观察我们发现，K01 轮密钥的生成已不再是通过三条指令加载出初始密钥将其与一个常量表异或了。而是通过四条指令加载出 K00 轮的第一组密钥，而其余三组的密钥则由上一组密钥与上一轮中的组密钥异或得到。下面，我们可以回顾下 AES 的标准密钥扩展算法得知到底是哪部分被魔改了。我们看看下面这两张图：

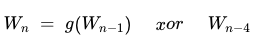
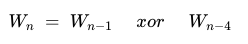
这里的 W 便代表我们所说的组，n 则等于（轮 - 1）* 4 + 4 = n。第一张图代表了每轮的第一组密钥生成规则，第二张图代表了每轮的其余三组生成规则。通过对比这两张图我们发现，第一组与其余组生成的规则多了个 g 函数。我们再观察上面的指令流得知，K01 轮的第二组的密钥是通过：

0x7dca99df ^ 0x9d357515 = 0xe0ffecca 得到，我们将这组数据代入我们的图2公式：

n = 00 * 4 + 4 = 4。而因为我们计算的是 K01 轮的第二组密钥，因此我们需要加上 1 。所以 n = 5。

W(5) = W(4) xor W(1)

W(4) = 0x7dca99df

W(1) = 0x9d357515

W(5) = 0x7dca99df xor 0x9d357515

W(5) = 0xe0ffecca

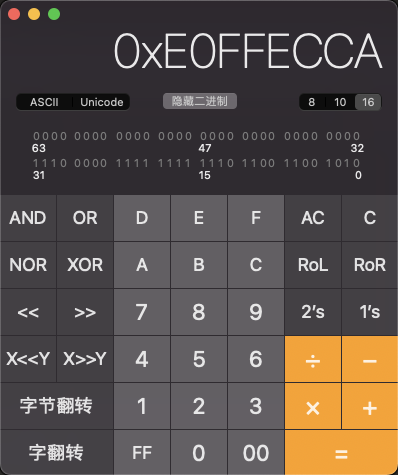
可以看到我们最后计算出来的值与在指令流中的值是一样的。因此我们可以断定，除了第一组密钥生成规则被魔改之外，其余组均未被魔改。所以接下来我们主要关注第一组密钥的生成。

我们通过对比知道第一组密钥的生成多了个 g 函数，因此我们要从汇编中将 g 函数的实现扣下来。现在我们回到 K01 轮第一组密钥的指令流中，我们将其生成的过程指令拿下来：

我们知道其中 0xc4eb1057 是 K00 轮中的第一组密钥，代入我们的图一公式可知：

W(4) = g(W(3)) xor W(0)

W3 = 0x970e7cf2

W0 = 0xc4eb1057

在这段指令流中我们看到 W0 的出现却没有发现 W3 的出现，并且多出了一串我们未曾见过的数据：

0xab000000 ^ 0x100000 ^ 0x8900 ^ 0x88 = 0xab108988

那么我们是不是可以假设 W3 被替换成了这串数据？那么这串数据怎么生成的就成了我们分析的关键。下面这部分指令是我从上万条指令中肉眼筛查出来的关键指令，这 6 条指令最终生成了 0xab000000 数据。

我们可以将这段汇编指令还原成伪 C 代码：

0x6dda0a3598 是我们的表基址，表基址加上偏移得到 0xabe64dab，再取 0xabe64dab 的高8位得到 0xab000000。偏移来自于 W3 的中高8位 * 4。因此，拿到表数据是我们还原的关键。那么怎么拿到表数据呢？我们可以通过指令的绝对地址减去相对地址得到 SO 的加载基址，再用表基址减去 SO 基址得到表在 SO 中的相对偏移。

0x6dda0a3598 - (0x6dd9feb83c - 0x2f83c) = 0xE7598。

我们在 IDA 中跳转到目标地址看看：

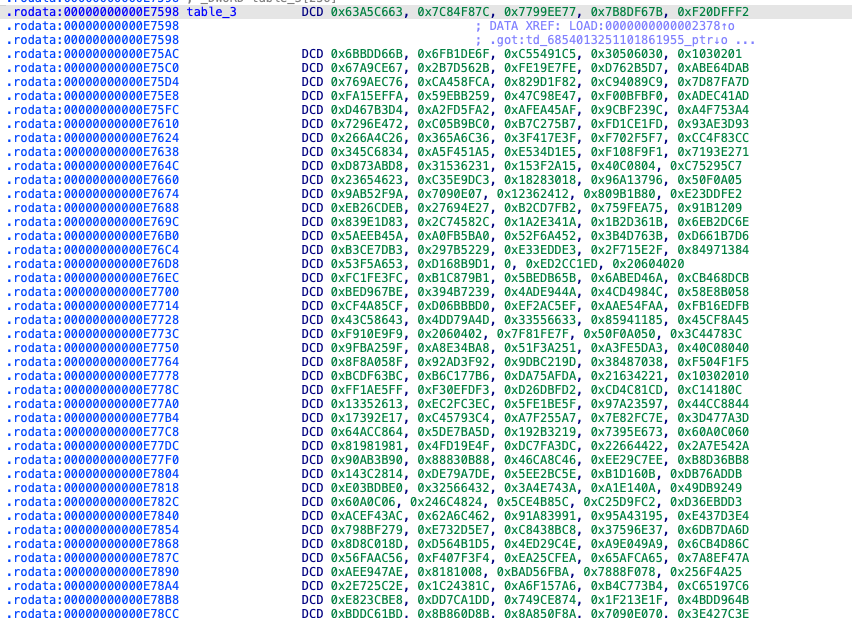
我们发现这个表正是我们在加密函数中看到的 table_3，并且可以看到表数据分别是 4 字节一组，对应我们的 offset = bword * 4 这行代码。至此我们可以将 W3 中高 8 位替换函数定义为：

现在我们知道了 W3 的中高 8 位替换公式，需要验证其他三个字节是不是也是相同的公式。这里我就不将指令流片段贴出来了，免得冗长。经过分析得到其余三个字节的替换公式：

我们通过观察这四个函数可以看到其具有一定的规律性，因此我们可以将其合并成一个函数：

现在我们拿到了 W3 的替换函数，就相当于完成了 0xab108988 ^ 0xc4eb1057 这一步，但是我们看到第一组密钥还与 0x12310000 进行异或才是我们最终的第一组密钥值。因此我们需要知道 0x12310000 是怎么生成的。

这里又经过了一番追溯，最终定位到这也是一个常量表中的值。因为这是固定的常量表，不影响我们后续的分析，所以就不写追溯过程了。

我们将这个常量表定义为 g_table：

接着我们观察这个常量表，发现长度是 10，恰好密钥扩展的轮数也是 10，那么是不是每一个元素对应每一轮扩展密钥的异或值？我们可以先这么假设将这个表融入到密钥扩展中，看看最终的生成出来的密钥是不是与指令流中的一致。

现在我们整理一下我们已知的所有信息：

初始密钥：35 62 31 66 62 35 64 36 2d 36 66 64 66 2d 34 62

IV：63 39 31 35 38 33 35 32 2d 61 30 30 37 2d 34 64

key_table、g_table、table_1、table_2、table_3、table_4

还有我们的替换函数 replace_key 与 密钥生成流程，所以我们现在可以根据这些已知的信息编写魔改后的密钥扩展算法：

上面是我将 4 个表数据抽空后的魔改密钥扩展算法。运行后得到如下输出：

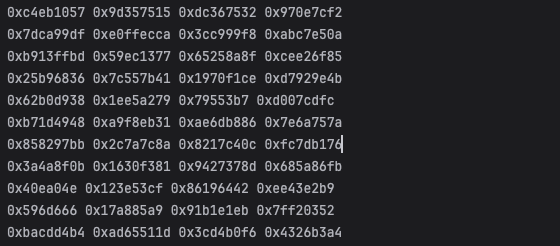
我们随机挑选两组密钥在指令流中搜索：

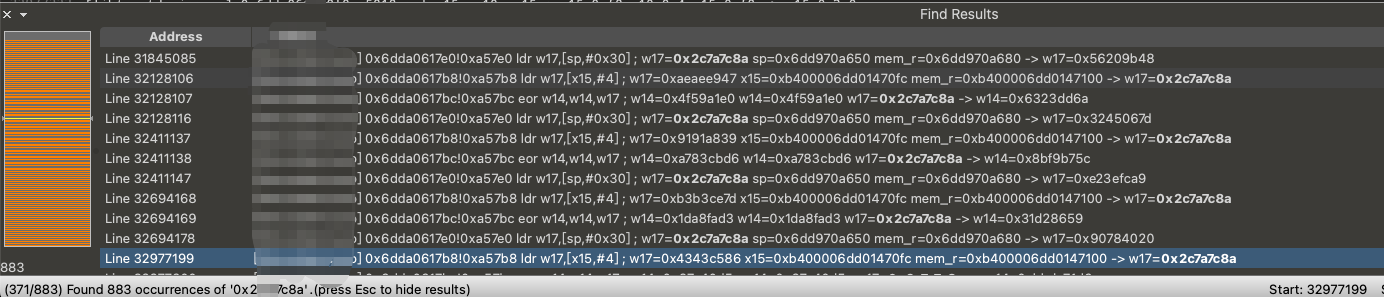
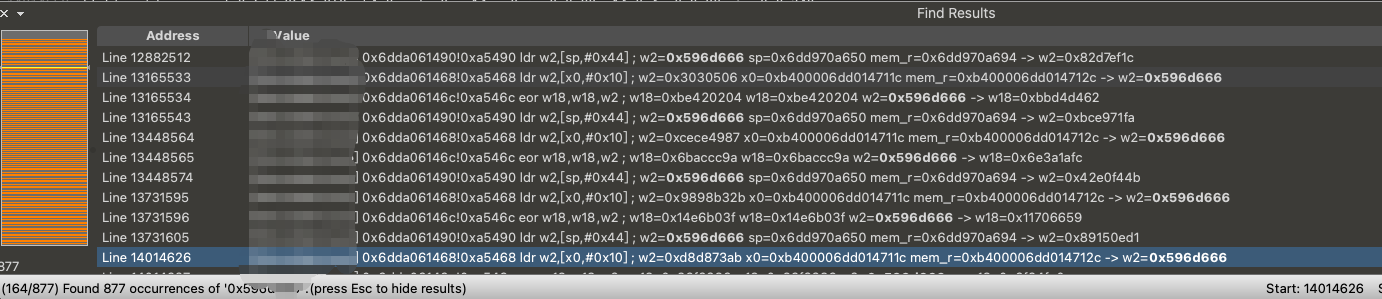
我们看到两组密钥都能搜到，证明我们的魔改密钥扩展算法还原成功了。

现在我们拿到了每一轮的密钥，并且我们已知这是个查表实现的 AES 128。那么我们只需要跟踪加密函数的汇编指令，将其中第一轮的轮加密过程给还原出来，就能通过相同的规则跑完剩下的 9 轮。我们将函数开头部分汇编指令拿下来

这是函数开头的初始轮密钥加与 state[0] 的计算过程指令流，用上下两个换行隔开是我添加的伪代码。从这部分指令流我们可以得出两个结论：

现在我们可以根据指令流将 state[0] 的计算过程整理为一个函数：

接着我又顺着指令流往下分析，得到了 state 中其余三个元素的函数：

我们观察这四个函数得知其具有一定规律性，计算的是哪个元素就用元素对应的下标做为查表的第一个元素。熟悉 AES 的朋友可能已经知道，这是在循环左移(shift_rows) 。所以我们可以将其合并为一个函数：

现在我们将明文与密钥结合起来跑一遍，得到如下输出：

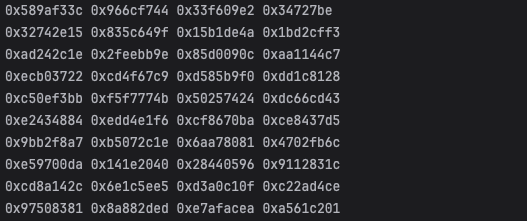
我们发现除了第十轮的密文不能在指令流中搜到，其余轮的密文都能搜到：

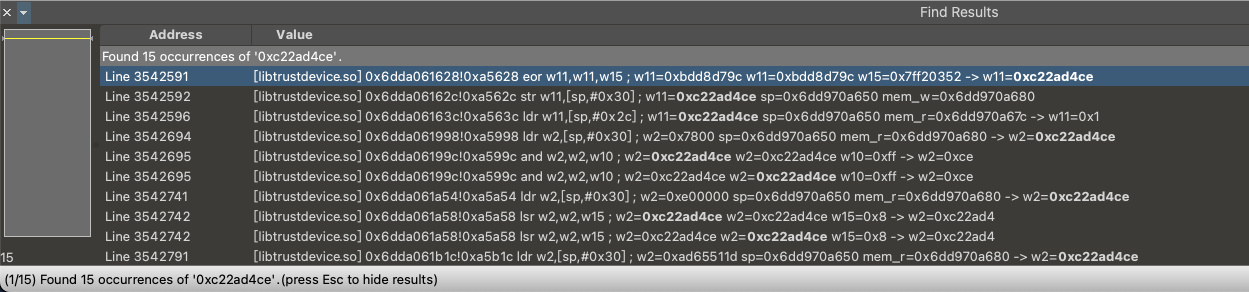
那也就是说第十轮的加密与我们整理出来的函数有出入。我们不妨回忆下标准 AES 的最后一轮前面的每轮有什么区别？是的，最后一轮没有列混淆。因此我们需要再次回到指令流中，将最后一轮的轮加密过程抠出来：

可以看到，最后一轮得到的 table_value 没有再与下一个元素得到的 table_value 进行异或。而是将他们从高 8 位取到低 8 位依次组成一个 32 位的 group_value 后直接与密钥异或得到我们的最终密文。接下来，我们根据指令流还原出最后一轮的加密函数：

我们运行后得到如下输出：

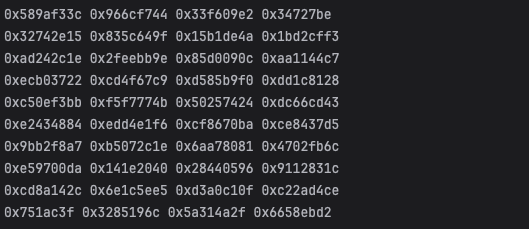
可以看到最后一轮的数据便是我们的最终密文，那么至此我们的算法就还原成功了。

事实上，在输入 AES 加密之前厂商还将数据进行了两轮 XOR 加密。但是，我们已经还原了 AES，XOR 就相对简单多了。这里考虑到厂商隐私安全的关系，我就不在文章中展开分析了。最后，贴一下未加密前的指纹数据：

建了个群感兴趣的朋友可以进来交流：

传播安全知识、拓宽行业人脉——看雪讲师团队等你加入！