-
-
[推荐]看雪.纽盾 KCTF 2019 Q3 | 第十题点评及解题思路
-
发表于: 2019-10-8 14:23 2976
-
胸怀大志的孙策希望能够有一天光宗耀祖。
父亲孙坚给了他一块玉玺并告诉他,只要他能打下2880座城镇,并在每个城镇祭拜玉玺,就能如愿。
孙策照着父亲的话去做了,最终赢得了胜利,并将这块玉玺视为传家宝。
袁术看见孙策成功了,也想模仿。
他日夜监视着孙策的动向,希望能够得到这件传家宝。
他能成功吗?

题目简介
本题共有916人围观,最终只有4支团队攻破成功。可见这道题的难度也十分大,出题者巧妙布局,引人步步深入,在破题的过程中方能见识到步步皆是棋局,走错一步满盘皆输。
攻破此题的战队排名一览:
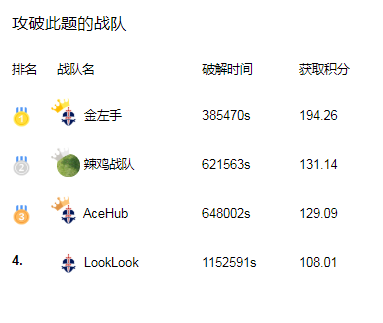
那么究竟出题者运用了什么巧妙战术,让我们一起来看一下吧。
看雪评委crownless点评
这题是一道Windows CrackMe,程序存在大量SMC,且嵌套2880层,很符合题目“传家之宝”的解释,考验了破解者写脚本破解的能力。但实际上,有另外的方法能直接提取核心aes代码。
出题团队简介
本题出题战队Archaia:

科锐学员队,即将毕业。
设计思路
此题设计特征如下:
所有数据都是明的,没有需要攻击者破解的数
所有数据的相互关系也是明的,没有隐晦的数学关系
所有解题所需的信息都在明处,没有隐藏任何线索
所有攻击者看到的线索都是真的,没有设置误导线索
所有指令都是会自动执行到的,没有需要寻找的代码
所有流程都很直白,没有异常,没有中断,没有回调
所有代码都是完整的,没有调用任何第三方API(接口部分除外)
有的,它只有一个难点:
长!然而,比赛已经限制了crackme的长度。蜗牛又能比别人长出来多少呢?
况且过去也有防守题codesize较大的。并未见到有哪道题是因为代码太长而无法被及时破解的。就算是市面上10+M,100+M的软件也都经常被破解。
长,能有多大用呢?其实,对于破解者来说,代码长不是问题。
因为破解者并无必要真的去阅读这些代码!大多数时候,破解者只需要“眼看手跳”就能快速pass大量无关破解的代码,直捣黄龙。所以,要想挡住破解者,不仅需要代码长,更重要的是:需要阻止“眼看手跳”!
设计思路
很简单,把代码加密了就行了。
代码一边运行一边解密(SMC),就能阻止眼看。如何阻止手跳呢?
所谓手跳,本质上就是下断点。调试方和反调试方围绕‘断点’展开的斗争,由来已久。
调试方的目标是:1)能断下2)能继续3)下次还能断下
为了做到这3点,调试方想出了很多招。在此不一一列举了。反调试方的目标只有1个:破坏调试条件。
只要破坏了调试方的调试条件,就能瞒天过海,不让调试方知道程序在干什么。同时,还不能影响正常业务流。
(这也是“薅羊毛”和“反薅羊毛”的主要战场)此题,为了阻止眼看手跳,引入了一种新加壳方式。我们称之为:
蜗牛壳始祖蜗牛以序列号作为起点,上路了。
蜗牛露头不多,但是背着一个大蜗牛壳。
蜗牛露出来的部分,肉很少,只负责往前走一小步,随即展开自己的蜗牛壳,抛出自己的下一代蜗牛。
下一代蜗牛,也背着一个蜗牛壳(稍微小一点)。
它露出来的部分,也有一点肉,也只负责往前走一小步,随即展开自己的蜗牛壳,再抛出自己的下一代蜗牛......
最后一代蜗牛,会检查自己是否走到了正确的目的地(是否命中了用户名)?
如果正确,则显示‘序列号正确’;否则显示‘错误’。用户输入的序列号,如同传家宝,在蜗牛家族里世代相传。
每一代蜗牛都坚守自己的使命,孵化序列号向前演进一小步,直到到达最终理想状态(输入的用户名)。
如果破解者能够看清每一代蜗牛在序列号上做的那么一小点孵化动作(露出来的那一片肉),并且全部拼装起来(变成一整块肉),就能知道如何从最终的用户名反向逆推出输入的序列号。反之,如果蜗牛家族能够不让对手看清某些蜗牛的动作(缺少几片肉),那么攻击者就很难找出逆推算法。
那么,蜗牛家族是如何让对手看不清的呢?
蜗牛壳技术要点
SMC加密
SMC技术能够有效防止破解者看到未来太远的代码。
解密算法和密钥,都在上一代的蜗牛体内,是破解者可以获得的。所以加密算法不必太强(强也没用)。只是一层障眼法而已,挡住肉眼就行了。比赛实践证明,这个技术对防护来说,贡献不大。至多只能当做一种辅助手段。
地址随机化
每一代蜗牛展开蜗牛壳,抛出下一代蜗牛时,随机指定下一代蜗牛的执行地址。
其目的是破坏调试目标3:“下次还能断下”比赛实践证明,这个地址随机化没能有效阻止高手的跟踪。要么被锁定了随机数,要么被动态跟踪。
切片技术
壳归壳,肉才是需要保护、不想被破解者看清的核心内容。
此题中所谓肉就是:从序列号到用户名的计算过程,原本是一段魔改AES代码(简称:AES_X)。
(注:这个计算过程一定要存在高效逆算法,否则出题方难以设计注册机)
需要将AES_X的代码切成切片,然后将每个切片贴到每层壳上。每层壳被执行的时候,相应的切片也会被执行。且需要保证:1)切片代码可以运行于任何内存地址(因为地址随机化了)2)每相邻2层切片之间的执行现场能够平顺衔接(不能被壳干扰)3)切片不可以循环,也最好不要分支(无分支编程技术,在这里发挥着重要作用)
有多少层壳,就切成多少片切片。如果层数大于指令数,就先对指令膨胀,然后再切片。
力图做到:破解者任意缺失了某个切片,都难以找出AES_X的逆运算。比赛实践证明,此题壳与肉的特征明显。对手找到后分离了壳和肉,去壳取肉。
代码独立
蜗牛壳在运作的时候,不调用任何外部的API,不使用外部的堆栈。代码执行时,不离开蜗牛壳。
这样设计的目的是:防止破解者在蜗牛壳之外设置断点,截获壳内信息。比赛实践证明,虽然我们试图回避壳内代码与外界的交互,但是却没提防破解者在壳内种植代码并逐层hook关键操作。而且,我们还是留下了一下操作外部数据的痕迹。就算是我们采用了内存校验,也难以保证校验代码不被patch掉。
对抗脚本
破解者在看了前面几层壳的架势之后,不会真的一层一层单步跟踪,而会写脚本脱壳取肉。
本题将多种反调试手段和数据变换,分级别部署在不同层的蜗牛壳中。每当遇到了新的反调试技,都需要破解者重新改写脚本,以延长破解时间。比赛实践证明,高手并未在反调试上花太多时间,且完全没有在数据变换上花任何时间。
总结与展望
《蜗牛的传家宝》文件长度:1,459,200字节核心代码:12902行源码工程:14400个文件(14.5GB)编译耗时:7小时(每次要编译,都要下个决心)反调试技:5种难度设计:10个级别数据变换:79种保护层数:2880层
此题招式朴实,没有高大上的算法,也没有机关算尽的诡计,不防单步跟踪,只是想让破解者‘飞’不起来而已。但是由于设计不完善,此题中留下了一系列比较致命的弱点,没能把破解者粘在地上,还是飞起来了。
我们将争取在下次参赛中弥补上这些漏洞。敬请期待。
解题思路
因为有代码段和栈的迁移,所以代码中不能硬编码绝对地址,都是相对当前EIP的相对偏移,所以取解码开始地址、取全局变量地址、EBP地址都是大多是根据当前EIP计算出来的,如下:
计算下一层代码入口地址,准备迁移代码并call执行
计算下一层代码入口地址,准备迁移代码并call执行 .text:0040171D E8 00 00 00 00 call $+5 .text:00401722 59 pop ecx .text:00401723 81 E9 48 10 40 00 sub ecx, 401048h .text:00401729 81 C1 43 11 40 00 add ecx, 401143h .text:0040172F E8 00 00 00 00 call $+5 .text:00401734 5F pop edi .text:00401735 81 EF 5A 10 40 00 sub edi, 40105Ah .text:0040173B 81 C7 10 10 40 00 add edi, 401010h 计算下一层解码开始地址 .text:00401845 E8 00 00 00 00 call $+5 .text:0040184A 5E pop esi .text:0040184B 81 EE 70 11 40 00 sub esi, 401170h .text:00401851 81 C6 01 12 40 00 add esi, 401201h .text:00401857 B9 27 CD 15 00 mov ecx, 15CD27h .text:0040185C FC cld .text:0040185D EB 1B jmp short loc_40187A 计算数据全局变量开始地址 .text:0040185F 9D popf .text:00401860 5F pop edi .text:00401861 5E pop esi .text:00401862 5A pop edx .text:00401863 59 pop ecx .text:00401864 5B pop ebx .text:00401865 58 pop eax .text:00401866 E8 00 00 00 00 call $+5 .text:0040186B 5E pop esi .text:0040186C 81 EE 91 11 40 00 sub esi, 401191h .text:00401872 81 C6 39 DF 55 00 add esi, 55DF39h .text:00401878 EB 05 jmp short loc_40187F 真实功能指令 .text:0040187F 8A 86 A7 01 00 00 mov al, [esi+1A7h] .text:00401885 32 86 B7 01 00 00 xor al, [esi+1B7h] .text:0040188B 88 45 FF mov [ebp-1], al
# -*- coding:utf-8 -*-
from __future__ import print_function
from idaapi import *
from idc import *
stop = False
def scan(patt,start=0,end=0):
pattern = patt
if start:
addr = start
else:
addr = MinEA()
if end:
addr1 = end
else:
addr1 = MaxEA()
for i in range(addr,addr1):
addr = FindBinary(addr, SEARCH_DOWN|SEARCH_NEXT, pattern)
if addr != BADADDR:
return addr
return 0
def get_saddr(addr):
while True:
addr = scan('E8 00 00 00 00 5e 81',start = addr,end=0x55e602)
if addr == 0:
return 0
if Byte(addr+12) == 0x81 and Byte(addr+18) == 0xb9:
return addr
elif Byte(addr+12) == 0x81 and Byte(addr+18) == 0xeb and Byte(addr+18+2+Byte(addr+18+1)) == 0xb9:
return addr
addr += 5
def patch_one_round(address,waddr):
SetRegValue(address,'eip')
addr = waddr+3
addr = scan('85 c9',start=addr,end=0x55e602)
if addr == 0:
return False
addr += 2
while Byte(addr) == 0xeb:
off = Byte(addr+1)
off = off if off < 0x80 else off - 0x100
addr += 2+off
if Byte(addr) == 0x75:
addr += 2
elif Word(addr) == 0x850f:
addr += 6
else:
return False
if addr - waddr > 0x100:
return False
AddBpt(addr)
EnableBpt(addr, True)
continue_process()
GetDebuggerEvent(WFNE_SUSP, -1)
DelBpt(addr)
return True
def patch_one_byte(address,waddr):
SetRegValue(address,'eip')
addr = waddr+3
AddBpt(addr)
EnableBpt(addr, True)
continue_process()
GetDebuggerEvent(WFNE_SUSP, -1)
DelBpt(addr)
return True
def quick_ALT_K(saddr = 0x40163E):
count = 0
# saddr = here()
while True:
print('start_addr:{:08X}'.format(saddr))
waddr = scan('88 46',start=saddr,end=0x55e602)
if waddr == 0 or waddr > 0x55e602 or Byte(waddr+2) not in [0x1,0xff]:
# waddr = scan('88 46 01',start=saddr,end=0x55e602)
print('waddr err or finished!')
break
print('waddr:{:08X}'.format(waddr))
if waddr - saddr < 10 or waddr - saddr > 0x100:
print('addr failed!')
break
addr_tmp = waddr+3
while Byte(addr_tmp) in [0xe9,0xeb]:
if Byte(addr_tmp) == 0xe9:
addr_tmp = (addr_tmp+5+Dword(addr_tmp+1))&0xffffffff
else:
off = Byte(addr_tmp+1)
off = off if off < 0x80 else off - 0x100
addr_tmp += 2+off
if Byte(addr_tmp) != 0x49:
patch_one_byte(saddr,waddr)
print('patch one byte')
else:
if not patch_one_round(saddr,waddr):
break
count += 1
if count % 500 == 0:
print(count)
save_database('crackme_fix_idb')
cur_ip = GetRegValue('eip')
print('curr_ip:{:08X}'.format(cur_ip))
for i in range(cur_ip,cur_ip+0x300):
MakeUnkn(i,0)
saddr = get_saddr(cur_ip-1)
if saddr == 0:
print('saddr err or finished!')
break
for i in range(0x4016A9,0x55e602):
MakeUnkn(i,0)
LoadDebugger('windbg',1)
AddBpt(0x40123F)
StartDebugger('','','')
GetDebuggerEvent(WFNE_SUSP, -1)
DelBpt(0x40123F)
quick_ALT_K()
#if AddHotkey("Alt+K","quick_ALT_K")!=IDCHK_OK:
# print('hotkey err!')
print('end.')解码后将无用代码nop掉了。发现SMC部分开始到到校验前都在一个函数中:
.text:00401663 000 E8 00 00 00 00 call $+5 .text:00401668 004 5E pop esi .text:00401669 000 81 EE 68 16 40 00 sub esi, 401668h .text:0040166F 000 81 C6 13 E6 55 00 add esi, offset table_256_55E613 .text:00401675 000 55 push ebp .text:00401676 004 8B EC mov ebp, esp .text:00401678 004 83 EC 2C sub esp, 2Ch .text:0055E0E6 030 83 C4 2C add esp, 2Ch .text:0055E0E9 004 8B E5 mov esp, ebp .text:0055E0EB 004 5D pop ebp .text:0055E0EC 000 E9 54 04 00 00 jmp j_check_55E545
v0 = t_190[4] ^ table_256_55E613[t_1a0[4] ^ result[4] ^ 9]; v1 = t_190[5] ^ table_256_55E613[t_1a0[1] ^ result[1] ^ 9]; v2 = t_190[6] ^ table_256_55E613[result[14] ^ t_1a0[14] ^ 9]; v3 = t_190[7] ^ table_256_55E613[result[11] ^ t_1a0[11] ^ 9]; v4 = t_190[8] ^ table_256_55E613[result[8] ^ t_1a0[8] ^ 9]; v5 = t_190[9] ^ table_256_55E613[(t_1a0[5] ^ result[5]) ^ 9]; v6 = t_190[10] ^ table_256_55E613[t_1a0[2] ^ result[2] ^ 9]; v7 = t_190[11] ^ table_256_55E613[result[15] ^ t_1a0[15] ^ 9]; v8 = t_190[12] ^ table_256_55E613[result[12] ^ t_1a0[12] ^ 9]; v9 = t_190[13] ^ table_256_55E613[(result[9] ^ t_1a0[9]) ^ 9]; v10 = t_190[14] ^ table_256_55E613[t_1a0[6] ^ result[6] ^ 9]; v11 = t_190[15] ^ table_256_55E613[t_1a0[3] ^ result[3] ^ 9]; v12 = t_190[0] ^ table_256_55E613[t_1a0[0] ^ result[0] ^ 9]; v13 = t_190[1] ^ table_256_55E613[result[13] ^ t_1a0[13] ^ 9]; v14 = t_190[2] ^ table_256_55E613[(result[10] ^ t_1a0[10]) ^ 9]; v15 = t_190[3] ^ table_256_55E613[(result[7] ^ t_1a0[7]) ^ 9]; v16 = 27 * (v12 >> 7); v17 = 27 * (v12 >> 7) ^ 2 * v12; v18 = 2 * v17 ^ 27 * (v17 >> 7); v19 = 27 * (v13 >> 7); v20 = 27 * (v13 >> 7) ^ 2 * v13; v21 = 27 * (v14 >> 7); v22 = 27 * (v14 >> 7) ^ 2 * v14; v23 = 27 * (v15 >> 7); v24 = 27 * (v15 >> 7) ^ 2 * v15; result[2] = aSnail3896q3405[2] ^ table_256_55E613[((t1_55E723[10] ^ v662) - 1)]; result[6] = aSnail3896q3405[6] ^ table_256_55E613[(v679 - 1)]; v689 = table_256_55E613[((t1_55E723[2] ^ v634) - 1)]; v690 = table_256_55E613[((t1_55E723[6] ^ v648) - 1)]; result[3] = aSnail3896q3405[3] ^ table_256_55E613[((t1_55E723[7] ^ v650) - 1)]; v691 = aSnail3896q3405[7] ^ table_256_55E613[((t1_55E723[11] ^ v664) - 1)]; result[4] = aSnail3896q3405[4] ^ v682; v692 = table_256_55E613[(v680 - 1)]; result[5] = aSnail3896q3405[5] ^ v686; result[8] = aSnail3896q3405[8] ^ v683; v693 = table_256_55E613[((t1_55E723[3] ^ v636) - 1)]; result[0] = aSnail3896q3405[0] ^ v681; result[1] = aSnail3896q3405[1] ^ v685; result[7] = v691; result[9] = aSnail3896q3405[9] ^ v687; result[12] = aSnail3896q3405[12] ^ v684; result[13] = aSnail3896q3405[13] ^ v688; result[10] = aSnail3896q3405[10] ^ v689; result[11] = aSnail3896q3405[11] ^ v692; result[15] = aSnail3896q3405[15] ^ v693; result[14] = aSnail3896q3405[14] ^ v690;
本想弄出个去除编码与无用代码且运行正常的程序,对原程序进行patch,发现计算结果不正确,折腾了两天也没找出是哪patch多了或少了。于是放弃。继续任务主线,解题。
在解代码前,测试过。输入的只要改动一个bit都会致使最后计算结果大相径庭,当时怀疑有对称加密。从伪代码可以很容易得出加密算法是AES。主要特征有计算过程中用到的256字节表及替换操作,最明显的是有限域的乘法代码。
v17=27*(v12 >>7) ^2*v12; v18=2*v17 ^27*(v17 >>7);
再将伪代码与AES算法进行对照,确定为AES算法无疑,只是作了修改。地址0x55E613开始的256字节表及后面的11组16字节表应该就是inv_sbox和round_key了。
很明显,add_round_key这部分被改了,行变换则没改。列混合变换一下一眼看不出来。调整了下伪代码,列出混合变换向量,发现列混合变换也没改。
//v14,v15,v16,v17为一行状态变量 v18 = 27 * (v14 >> 7); v19 = 27 * (v14 >> 7) ^ 2 * v14; v20 = 2 * v19 ^ 27 * (v19 >> 7); v21 = 27 * (v15 >> 7); v22 = 27 * (v15 >> 7) ^ 2 * v15; v23 = 27 * (v16 >> 7); v24 = 27 * (v16 >> 7) ^ 2 * v16; v25 = 27 * (v17 >> 7); v26 = 27 * (v17 >> 7) ^ 2 * v17; v27 = v16 ^ v15 ^ v18 ^ 2 * v14 ^ v21 ^ 2 * v15 ^ v17 ^ 27 * (v19 >> 7) ^ 2 * v19 ^ 27 * (v20 >> 7) ^ 2 * v20 ^ 27 * ((2 * v22 ^ 27 * (v22 >> 7)) >> 7) ^ 2 * 2 * v22 ^ 27 * (v22 >> 7) ^ 27 * (v24 >> 7) ^ 2 * v24 ^ 27 * ((2 * v24 ^ 27 * (v24 >> 7)) >> 7) ^ 2 * 2 * v24 ^ 27 * (v24 >> 7) ^ 27 * ((2 * v26 ^ 27 * (v26 >> 7)) >> 7) ^ 2 * 2 * v26 ^ 27 * (v26 >> 7) 1110 14 E 1011 11 B 1101 13 D 1001 9 9
# -*- coding:utf-8 -*-
Sbox = (
0x90,0x75,0xB4,0x69,0x59,0x47,0x97,0xC6,0x1A,0xC2,0x3A,0xA9,0x0E,0x05,0xBB,0x21,
0xB9,0xBA,0x9B,0x92,0xCE,0xF2,0x6B,0xEB,0x7A,0x8F,0xE9,0x14,0xE1,0x61,0x06,0x5F,
0x87,0xE6,0x80,0xDE,0x45,0xA6,0x22,0x37,0x9A,0x50,0x39,0x49,0x8D,0x02,0xD6,0x04,
0x15,0x13,0x2F,0x53,0x8C,0xD1,0xD7,0x34,0x60,0xB0,0x93,0x66,0xF0,0xE4,0xD5,0x63,
0x1E,0x2C,0x83,0x30,0x4C,0x99,0xBD,0x8B,0xDD,0x9F,0x31,0x44,0x74,0xF9,0x23,0xAA,
0xC3,0x96,0xF6,0xCF,0x9D,0x88,0x41,0xF5,0x4E,0xAE,0xFF,0xE5,0x9E,0x1B,0x48,0xED,
0x7E,0xDF,0x84,0x2D,0x3D,0x32,0x3C,0x0F,0x36,0xE3,0xD8,0x17,0xA5,0x33,0x3B,0x94,
0xE8,0xD3,0x16,0xD4,0x7D,0x20,0x6D,0x5B,0x0D,0xE7,0x42,0x7C,0xF4,0xBE,0x1C,0xBF,
0x56,0x65,0xC7,0x4F,0xC0,0x6F,0xB3,0x7F,0x81,0x2A,0xD0,0x43,0x73,0x62,0xD9,0x64,
0x07,0xC4,0xEC,0xA1,0xF7,0xA7,0x76,0xFC,0x2E,0xC8,0x54,0xAF,0x26,0xF8,0x57,0x86,
0xB5,0x4D,0x67,0x25,0xF1,0x72,0x1F,0x70,0x01,0xA3,0x95,0x5D,0x98,0xAC,0x27,0xC1,
0xB6,0xEE,0xCC,0x38,0x71,0xB2,0x6A,0x2B,0x8E,0xCD,0x10,0x55,0x0C,0xAD,0xCB,0x78,
0x82,0x08,0x0A,0x46,0xF3,0x3F,0x77,0xC5,0x51,0x52,0x29,0x24,0x3E,0x5A,0xA0,0x35,
0x5C,0x4B,0xE0,0xE2,0x58,0x11,0x00,0xFE,0xA4,0x8A,0x0B,0xCA,0xDB,0x79,0x68,0x4A,
0x9C,0x5E,0x91,0x03,0x7B,0x19,0x6C,0xA8,0xC9,0x09,0xB7,0xA2,0xFA,0xEA,0x89,0xEF,
0x18,0xDC,0x28,0xBC,0xD2,0xFD,0xDA,0x1D,0xB1,0x6E,0xFB,0x85,0x12,0xB8,0xAB,0x40,
)
InvSbox = (
0xD6,0xA8,0x2D,0xE3,0x2F,0x0D,0x1E,0x90,0xC1,0xE9,0xC2,0xDA,0xBC,0x78,0x0C,0x67,
0xBA,0xD5,0xFC,0x31,0x1B,0x30,0x72,0x6B,0xF0,0xE5,0x08,0x5D,0x7E,0xF7,0x40,0xA6,
0x75,0x0F,0x26,0x4E,0xCB,0xA3,0x9C,0xAE,0xF2,0xCA,0x89,0xB7,0x41,0x63,0x98,0x32,
0x43,0x4A,0x65,0x6D,0x37,0xCF,0x68,0x27,0xB3,0x2A,0x0A,0x6E,0x66,0x64,0xCC,0xC5,
0xFF,0x56,0x7A,0x8B,0x4B,0x24,0xC3,0x05,0x5E,0x2B,0xDF,0xD1,0x44,0xA1,0x58,0x83,
0x29,0xC8,0xC9,0x33,0x9A,0xBB,0x80,0x9E,0xD4,0x04,0xCD,0x77,0xD0,0xAB,0xE1,0x1F,
0x38,0x1D,0x8D,0x3F,0x8F,0x81,0x3B,0xA2,0xDE,0x03,0xB6,0x16,0xE6,0x76,0xF9,0x85,
0xA7,0xB4,0xA5,0x8C,0x4C,0x01,0x96,0xC6,0xBF,0xDD,0x18,0xE4,0x7B,0x74,0x60,0x87,
0x22,0x88,0xC0,0x42,0x62,0xFB,0x9F,0x20,0x55,0xEE,0xD9,0x47,0x34,0x2C,0xB8,0x19,
0x00,0xE2,0x13,0x3A,0x6F,0xAA,0x51,0x06,0xAC,0x45,0x28,0x12,0xE0,0x54,0x5C,0x49,
0xCE,0x93,0xEB,0xA9,0xD8,0x6C,0x25,0x95,0xE7,0x0B,0x4F,0xFE,0xAD,0xBD,0x59,0x9B,
0x39,0xF8,0xB5,0x86,0x02,0xA0,0xB0,0xEA,0xFD,0x10,0x11,0x0E,0xF3,0x46,0x7D,0x7F,
0x84,0xAF,0x09,0x50,0x91,0xC7,0x07,0x82,0x99,0xE8,0xDB,0xBE,0xB2,0xB9,0x14,0x53,
0x8A,0x35,0xF4,0x71,0x73,0x3E,0x2E,0x36,0x6A,0x8E,0xF6,0xDC,0xF1,0x48,0x23,0x61,
0xD2,0x1C,0xD3,0x69,0x3D,0x5B,0x21,0x79,0x70,0x1A,0xED,0x17,0x92,0x5F,0xB1,0xEF,
0x3C,0xA4,0x15,0xC4,0x7C,0x57,0x52,0x94,0x9D,0x4D,0xEC,0xFA,0x97,0xF5,0xD7,0x5A,
)
# learnt from ecdK9s2c8@1M7q4)9K6b7g2)9J5c8W2)9J5c8X3y4K6i4K6u0W2N6h3y4K6j5W2)9J5k6h3g2V1N6g2)9J5c8W2)9%4c8h3E0G2j5#2)9J5c8X3y4K6x3e0M7^5i4K6u0r3M7s2u0G2K9X3g2U0N6s2y4Q4x3V1k6v1g2q4)9J5c8X3q4W2M7#2)9J5k6h3x3`.
xtime = lambda a: (((a << 1) ^ 0x1B) & 0xFF) if (a & 0x80) else (a << 1)
Rcon = (
0x00, 0x01, 0x02, 0x04, 0x08, 0x10, 0x20, 0x40,
0x80, 0x1B, 0x36, 0x6C, 0xD8, 0xAB, 0x4D, 0x9A,
0x2F, 0x5E, 0xBC, 0x63, 0xC6, 0x97, 0x35, 0x6A,
0xD4, 0xB3, 0x7D, 0xFA, 0xEF, 0xC5, 0x91, 0x39,
)
def text2matrix(text):
matrix = []
for i in range(16):
byte = (text >> (8 * (15 - i))) & 0xFF
if i % 4 == 0:
matrix.append([byte])
else:
matrix[i / 4].append(byte)
return matrix
def matrix2text(matrix):
text = 0
for i in range(4):
for j in range(4):
text |= (matrix[i][j] << (120 - 8 * (4 * i + j)))
return text
class AES:
def __init__(self, master_key):
# self.change_key(master_key)
self.round_keys = [
[0x73,0x6E,0x61,0x69],[0x6C,0x33,0x38,0x39],[0x36,0x71,0x33,0x34],[0x30,0x35,0x25,0x00],
[0xE4,0x51,0x1D,0x6D],[0x88,0x62,0x25,0x54],[0xBE,0x13,0x16,0x60],[0x8E,0x26,0x33,0x60],
[0x11,0x92,0xCD,0x74],[0x99,0xF0,0xE8,0x20],[0x27,0xE3,0xFE,0x40],[0xA9,0xC5,0xCD,0x20],
[0xB3,0x2F,0x7A,0xA7],[0x2A,0xDF,0x92,0x87],[0x0D,0x3C,0x6C,0xC7],[0xA4,0xF9,0xA1,0xE7],
[0x22,0x1D,0xEE,0xEE],[0x08,0xC2,0x7C,0x69],[0x05,0xFE,0x10,0xAE],[0xA1,0x07,0xB1,0x49],
[0xF7,0xD5,0xD5,0xDC],[0xFF,0x17,0xA9,0xB5],[0xFA,0xE9,0xB9,0x1B],[0x5B,0xEE,0x08,0x52],
[0xFF,0xE5,0xD5,0xE5],[0x00,0xF2,0x7C,0x50],[0xFA,0x1B,0xC5,0x4B],[0xA1,0xF5,0xCD,0x19],
[0x59,0x58,0x01,0xD7],[0x59,0xAA,0x7D,0x87],[0xA3,0xB1,0xB8,0xCC],[0x02,0x44,0x75,0xD5],
[0xC2,0xC5,0x02,0xA0],[0x9B,0x6F,0x7F,0x27],[0x38,0xDE,0xC7,0xEB],[0x3A,0x9A,0xB2,0x3E],
[0x61,0xF2,0xB0,0x20],[0xFA,0x9D,0xCF,0x07],[0xC2,0x43,0x08,0xEC],[0xF8,0xD9,0xBA,0xD2],
[0x62,0x06,0x05,0x61],[0x98,0x9B,0xCA,0x66],[0x5A,0xD8,0xC2,0x8A],[0xA2,0x01,0x78,0x58]
]
def encrypt(self, plaintext):
self.plain_state = text2matrix(plaintext)
self.__add_round_key(self.plain_state, self.round_keys[:4])
self.__sub_bytes(self.plain_state)
self.__trans_row_col(self.plain_state)
self.__shift_rows(self.plain_state)
self.__trans_row_col(self.plain_state)
self.plain_state = map(lambda x:map(lambda y:(y+1)&0xff,x),self.plain_state)
self.__add_round_key(self.plain_state, self.round_keys[4:8])
self.__mix_columns(self.plain_state)
self.__sub_bytes(self.plain_state)
self.__trans_row_col(self.plain_state)
self.__shift_rows(self.plain_state)
self.__trans_row_col(self.plain_state)
self.plain_state = map(lambda x:map(lambda y:(y+2)&0xff,x),self.plain_state)
self.__mix_columns(self.plain_state)
self.__add_round_key(self.plain_state, self.round_keys[8:12])
self.__sub_bytes(self.plain_state)
self.__trans_row_col(self.plain_state)
self.__shift_rows(self.plain_state)
self.__trans_row_col(self.plain_state)
self.plain_state = map(lambda x:map(lambda y:y^9,x),self.plain_state)
self.__add_round_key(self.plain_state, self.round_keys[12:16])
self.__mix_columns(self.plain_state)
self.__sub_bytes(self.plain_state)
self.__trans_row_col(self.plain_state)
self.__shift_rows(self.plain_state)
self.__trans_row_col(self.plain_state)
self.plain_state = map(lambda x:map(lambda y:y^7,x),self.plain_state)
self.__mix_columns(self.plain_state)
self.__add_round_key(self.plain_state, self.round_keys[16:20])
self.__sub_bytes(self.plain_state)
self.__trans_row_col(self.plain_state)
self.__shift_rows(self.plain_state)
self.__trans_row_col(self.plain_state)
self.plain_state = map(lambda x:map(lambda y:(y-1)&0xff,x),self.plain_state)
self.__add_round_key(self.plain_state, self.round_keys[20:24])
self.__mix_columns(self.plain_state)
self.__sub_bytes(self.plain_state)
self.__trans_row_col(self.plain_state)
self.__shift_rows(self.plain_state)
self.__trans_row_col(self.plain_state)
self.plain_state = map(lambda x:map(lambda y:y^3,x),self.plain_state)
self.__mix_columns(self.plain_state)
self.__add_round_key(self.plain_state, self.round_keys[24:28])
self.__sub_bytes(self.plain_state)
self.__trans_row_col(self.plain_state)
self.__shift_rows(self.plain_state)
self.__trans_row_col(self.plain_state)
self.plain_state = map(lambda x:map(lambda y:y^8,x),self.plain_state)
self.__mix_columns(self.plain_state)
self.__add_round_key(self.plain_state, self.round_keys[28:32])
self.__sub_bytes(self.plain_state)
self.__trans_row_col(self.plain_state)
self.__shift_rows(self.plain_state)
self.__trans_row_col(self.plain_state)
self.plain_state = map(lambda x:map(lambda y:y^6,x),self.plain_state)
self.__add_round_key(self.plain_state, self.round_keys[32:36])
self.__mix_columns(self.plain_state)
self.__sub_bytes(self.plain_state)
self.__trans_row_col(self.plain_state)
self.__shift_rows(self.plain_state)
self.__trans_row_col(self.plain_state)
self.__mix_columns(self.plain_state)
self.__add_round_key(self.plain_state, self.round_keys[36:40])
self.__sub_bytes(self.plain_state)
self.__trans_row_col(self.plain_state)
self.__shift_rows(self.plain_state)
self.__trans_row_col(self.plain_state)
self.plain_state = map(lambda x:map(lambda y:y^9,x),self.plain_state)
self.__add_round_key(self.plain_state, self.round_keys[40:])
return matrix2text(self.plain_state)
def decrypt(self, ciphertext):
self.cipher_state = text2matrix(ciphertext)
self.__add_round_key(self.cipher_state, self.round_keys[40:])
self.cipher_state = map(lambda x:map(lambda y:y^9,x),self.cipher_state)
self.__trans_row_col(self.cipher_state)
self.__inv_shift_rows(self.cipher_state)
self.__trans_row_col(self.cipher_state)
self.__inv_sub_bytes(self.cipher_state)
self.__add_round_key(self.cipher_state, self.round_keys[36:40])
self.__inv_mix_columns(self.cipher_state)
self.__trans_row_col(self.cipher_state)
self.__inv_shift_rows(self.cipher_state)
self.__trans_row_col(self.cipher_state)
self.__inv_sub_bytes(self.cipher_state)
self.__inv_mix_columns(self.cipher_state)
self.__add_round_key(self.cipher_state, self.round_keys[32:36])
self.cipher_state = map(lambda x:map(lambda y:y^6,x),self.cipher_state)
self.__trans_row_col(self.cipher_state)
self.__inv_shift_rows(self.cipher_state)
self.__trans_row_col(self.cipher_state)
self.__inv_sub_bytes(self.cipher_state)
self.__add_round_key(self.cipher_state, self.round_keys[28:32])
self.__inv_mix_columns(self.cipher_state)
self.cipher_state = map(lambda x:map(lambda y:y^8,x),self.cipher_state)
self.__trans_row_col(self.cipher_state)
self.__inv_shift_rows(self.cipher_state)
self.__trans_row_col(self.cipher_state)
self.__inv_sub_bytes(self.cipher_state)
self.__add_round_key(self.cipher_state, self.round_keys[24:28])
self.__inv_mix_columns(self.cipher_state)
self.cipher_state = map(lambda x:map(lambda y:y^3,x),self.cipher_state)
self.__trans_row_col(self.cipher_state)
self.__inv_shift_rows(self.cipher_state)
self.__trans_row_col(self.cipher_state)
self.__inv_sub_bytes(self.cipher_state)
self.__inv_mix_columns(self.cipher_state)
self.__add_round_key(self.cipher_state, self.round_keys[20:24])
self.cipher_state = map(lambda x:map(lambda y:(y+1)&0xff,x),self.cipher_state)
self.__trans_row_col(self.cipher_state)
self.__inv_shift_rows(self.cipher_state)
self.__trans_row_col(self.cipher_state)
self.__inv_sub_bytes(self.cipher_state)
self.__add_round_key(self.cipher_state, self.round_keys[16:20])
self.__inv_mix_columns(self.cipher_state)
self.cipher_state = map(lambda x:map(lambda y:y^7,x),self.cipher_state)
self.__trans_row_col(self.cipher_state)
self.__inv_shift_rows(self.cipher_state)
self.__trans_row_col(self.cipher_state)
self.__inv_sub_bytes(self.cipher_state)
self.__inv_mix_columns(self.cipher_state)
self.__add_round_key(self.cipher_state, self.round_keys[12:16])
self.cipher_state = map(lambda x:map(lambda y:y^9,x),self.cipher_state)
self.__trans_row_col(self.cipher_state)
self.__inv_shift_rows(self.cipher_state)
self.__trans_row_col(self.cipher_state)
self.__inv_sub_bytes(self.cipher_state)
self.__add_round_key(self.cipher_state, self.round_keys[8:12])
self.__inv_mix_columns(self.cipher_state)
self.cipher_state = map(lambda x:map(lambda y:(y-2)&0xff,x),self.cipher_state)
self.__trans_row_col(self.cipher_state)
self.__inv_shift_rows(self.cipher_state)
self.__trans_row_col(self.cipher_state)
self.__inv_sub_bytes(self.cipher_state)
self.__inv_mix_columns(self.cipher_state)
self.__add_round_key(self.cipher_state, self.round_keys[4:8])
self.cipher_state = map(lambda x:map(lambda y:(y-1)&0xff,x),self.cipher_state)
self.__trans_row_col(self.cipher_state)
self.__inv_shift_rows(self.cipher_state)
self.__trans_row_col(self.cipher_state)
self.__inv_sub_bytes(self.cipher_state)
self.__add_round_key(self.cipher_state, self.round_keys[:4])
return matrix2text(self.cipher_state)
def __add_round_key(self, s, k):
for i in range(4):
for j in range(4):
s[i][j] ^= k[i][j]
def __round_encrypt(self, state_matrix, key_matrix):
self.__sub_bytes(state_matrix)
self.__shift_rows(state_matrix)
self.__mix_columns(state_matrix)
self.__add_round_key(state_matrix, key_matrix)
def __round_decrypt(self, state_matrix, key_matrix):
self.__add_round_key(state_matrix, key_matrix)
self.__inv_mix_columns(state_matrix)
self.__inv_shift_rows(state_matrix)
self.__inv_sub_bytes(state_matrix)
def __sub_bytes(self, s):
for i in range(4):
for j in range(4):
s[i][j] = Sbox[s[i][j]]
def __trans_row_col(self,s):
t1 = s[0][0], s[1][0], s[2][0], s[3][0]
t2 = s[0][1], s[1][1], s[2][1], s[3][1]
t3 = s[0][2], s[1][2], s[2][2], s[3][2]
t4 = s[0][3], s[1][3], s[2][3], s[3][3]
s[0][0], s[0][1], s[0][2], s[0][3] = t1[0], t1[1], t1[2], t1[3]
s[1][0], s[1][1], s[1][2], s[1][3] = t2[0], t2[1], t2[2], t2[3]
s[2][0], s[2][1], s[2][2], s[2][3] = t3[0], t3[1], t3[2], t3[3]
s[3][0], s[3][1], s[3][2], s[3][3] = t4[0], t4[1], t4[2], t4[3]
def __inv_sub_bytes(self, s):
for i in range(4):
for j in range(4):
s[i][j] = InvSbox[s[i][j]]
def __shift_rows(self, s):
s[1][0], s[1][1], s[1][2], s[1][3] = s[1][1], s[1][2],s[1][3],s[1][0]
s[2][0], s[2][1], s[2][2], s[2][3] = s[2][2],s[2][3],s[2][0], s[2][1]
s[3][0], s[3][1], s[3][2], s[3][3] = s[3][3], s[3][0],s[3][1],s[3][2]
def __inv_shift_rows(self, s):
s[1][0], s[1][1], s[1][2], s[1][3] = s[1][3], s[1][0], s[1][1], s[1][2]
s[2][0], s[2][1], s[2][2], s[2][3] = s[2][2], s[2][3], s[2][0], s[2][1]
s[3][0], s[3][1], s[3][2], s[3][3] = s[3][1], s[3][2], s[3][3], s[3][0]
def __mix_single_column(self, a):
# please see Sec 4.1.2 in The Design of Rijndael
t = a[0] ^ a[1] ^ a[2] ^ a[3]
u = a[0]
a[0] ^= t ^ xtime(a[0] ^ a[1])
a[1] ^= t ^ xtime(a[1] ^ a[2])
a[2] ^= t ^ xtime(a[2] ^ a[3])
a[3] ^= t ^ xtime(a[3] ^ u)
def __mix_columns(self, s):
for i in range(4):
self.__mix_single_column(s[i])
def __inv_mix_columns(self, s):
# see Sec 4.1.3 in The Design of Rijndael
for i in range(4):
u = xtime(xtime(s[i][0] ^ s[i][2]))
v = xtime(xtime(s[i][1] ^ s[i][3]))
s[i][0] ^= u
s[i][1] ^= v
s[i][2] ^= u
s[i][3] ^= v
self.__mix_columns(s)
if __name__ == '__main__':
cipher = AES(0)
m = cipher.decrypt(int('C0B10D687FAB692FFED16BDFFBF2BA2E',16))
print hex(m)[2:].replace('L','')#.decode('hex')
m = 'KCTF'+'\x00'*12
# m = 'B54333CE90874B76'
c = cipher.encrypt(int(m.encode('hex'),16))
print hex(c)[2:].replace('L','').upper()1.2880层解码,有以量取胜的嫌疑,通常情况下做题者不喜。
2.只要模式较固定,脚本解码就有了可能。
[培训]传播安全知识、拓宽行业人脉——看雪讲师团队等你加入!