-
-
[原创]静态程序分析之数据流分析(Application + Foundations)
-
发表于: 2025-10-10 16:49
-
各位大侠好这是我的静态程序分析笔记，主要分为两个部分
1. Application
2. Foundations
如果各位只是了解常见的分析算法可以只看应用部分，理论部分仅作了解即可，如果有什么不对恳请各位大侠在评论区指出错误。
Static Program Analysis Introduction
PL通常有3个组成
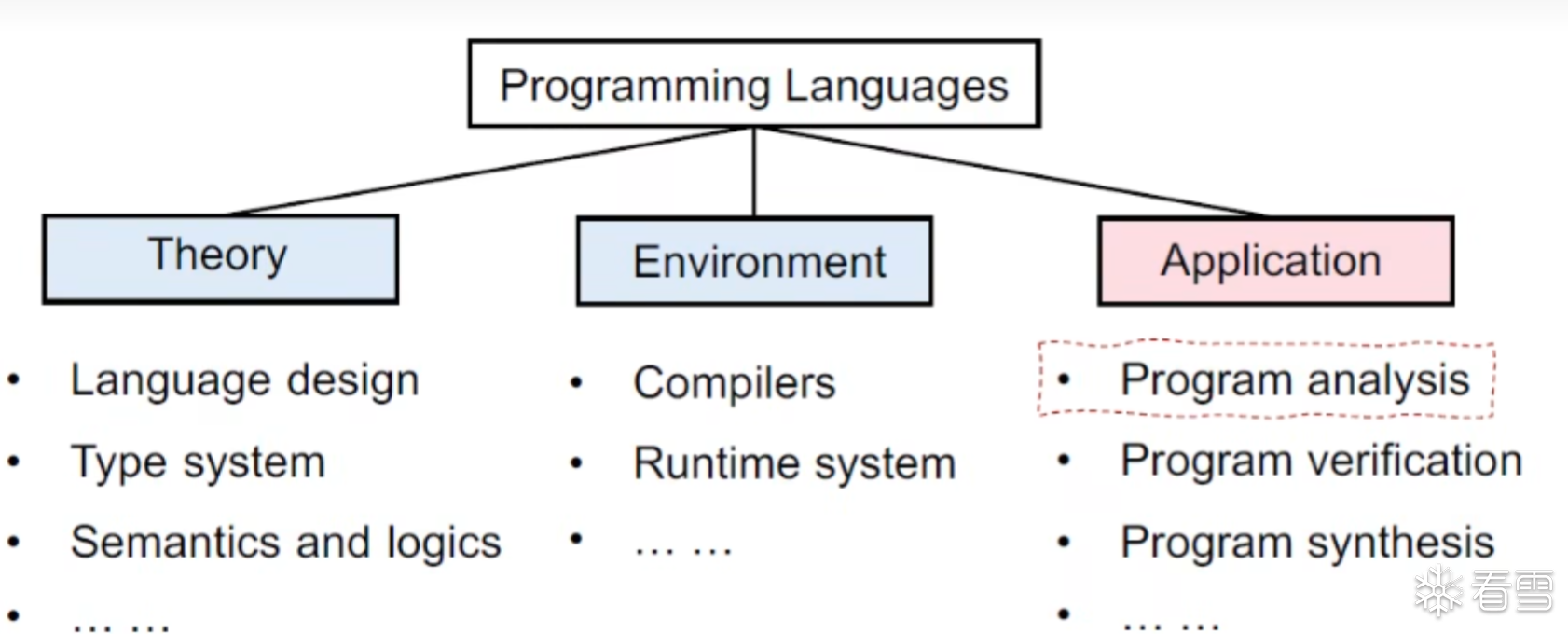
语言的类别
语言的发展语言没有变，但是语用环境变了即需求变复杂了，软件也变得很复杂，我们需要保证在复杂程序下的可靠性和安全性。
但是根据 Rice's Theorem 理论不能存在准确的告诉我们是否存在上述问题
non-trivial 不简单的属性是不能被判断的，不简单的可以简单理解为和动态运行时相关的一些属性。
通俗来讲就是，但凡是递归类型的语言，当我们在想要获取动态运行时的一些属性的时候，是不存在确定性的结论的。
完美静态分析所具有的特性
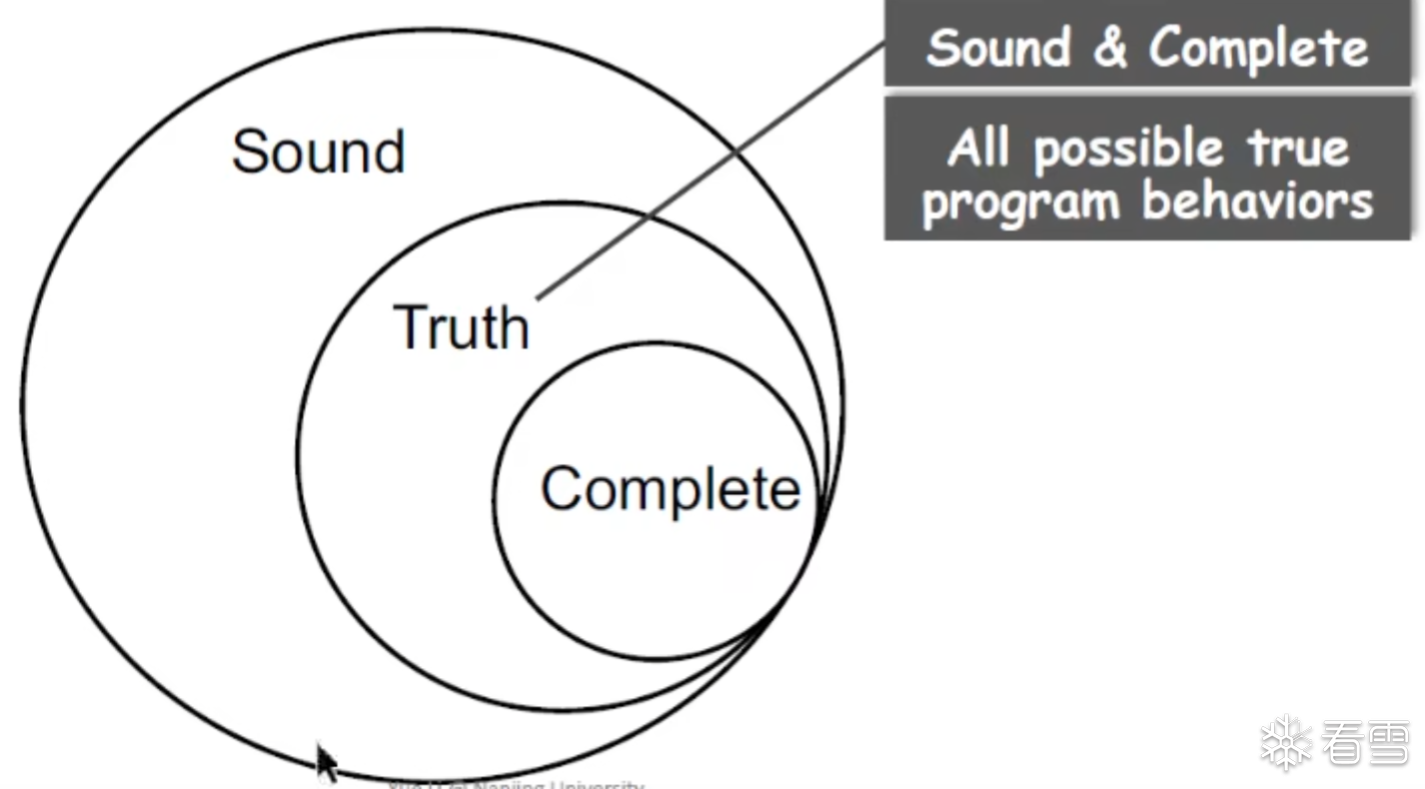
根据Rice定理不存在即Sound 又 Complete的Perfect static analysis
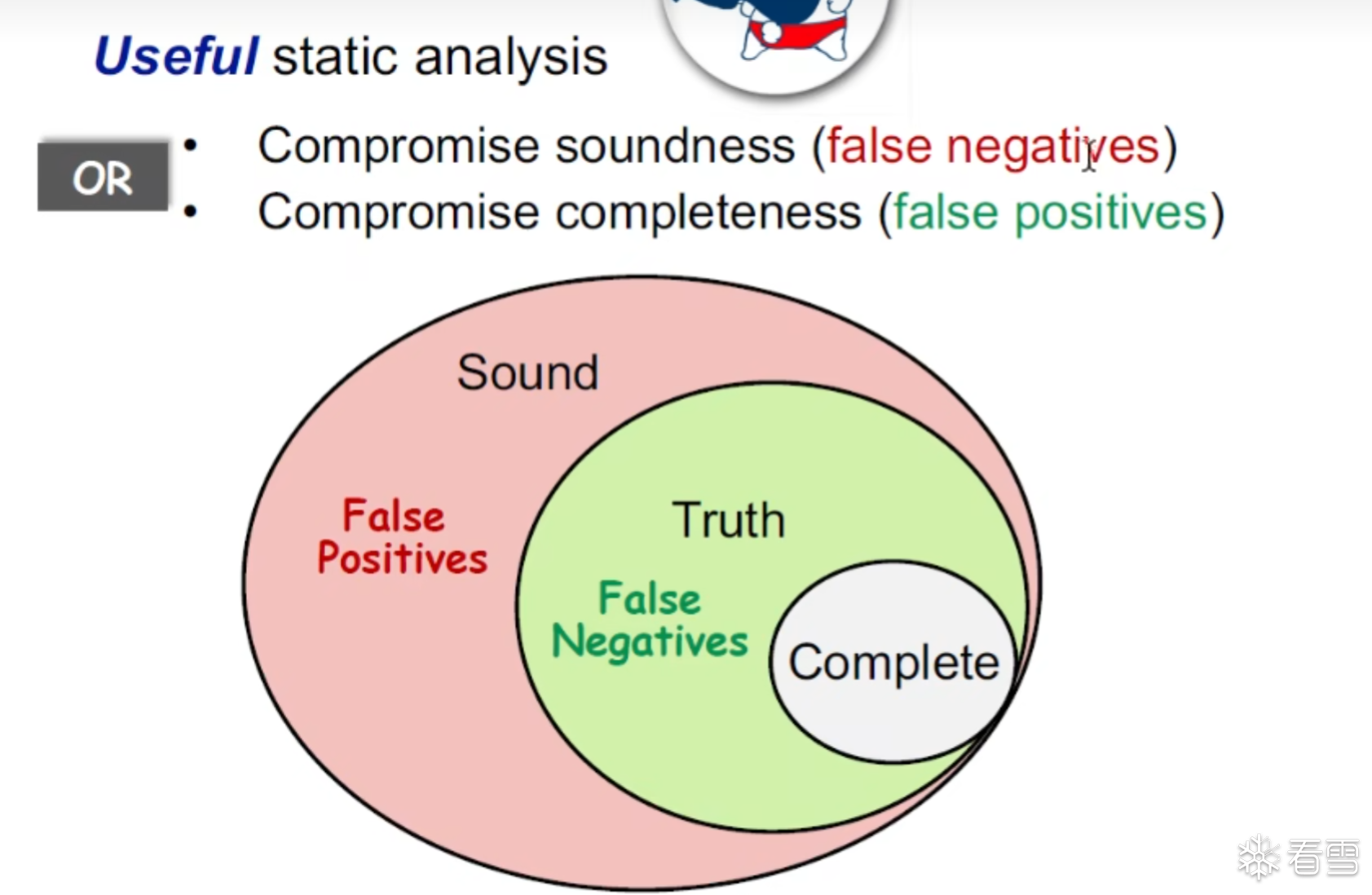
即一个漏报一个误报，两种妥协方式。
但是在真实的分析过程中我们一般只妥协Complete 而不妥协 Sound。
健壮性对于一系列重要的(静态分析)应用至关重要。下面的例子来体现出 Sound 路径
需要在精度和速度时候做出平衡
譬如我们给出如下任务判断所有的变量的正负
我们要把关心的值抽象到我们域中去，这个f(x)标识了这个映射
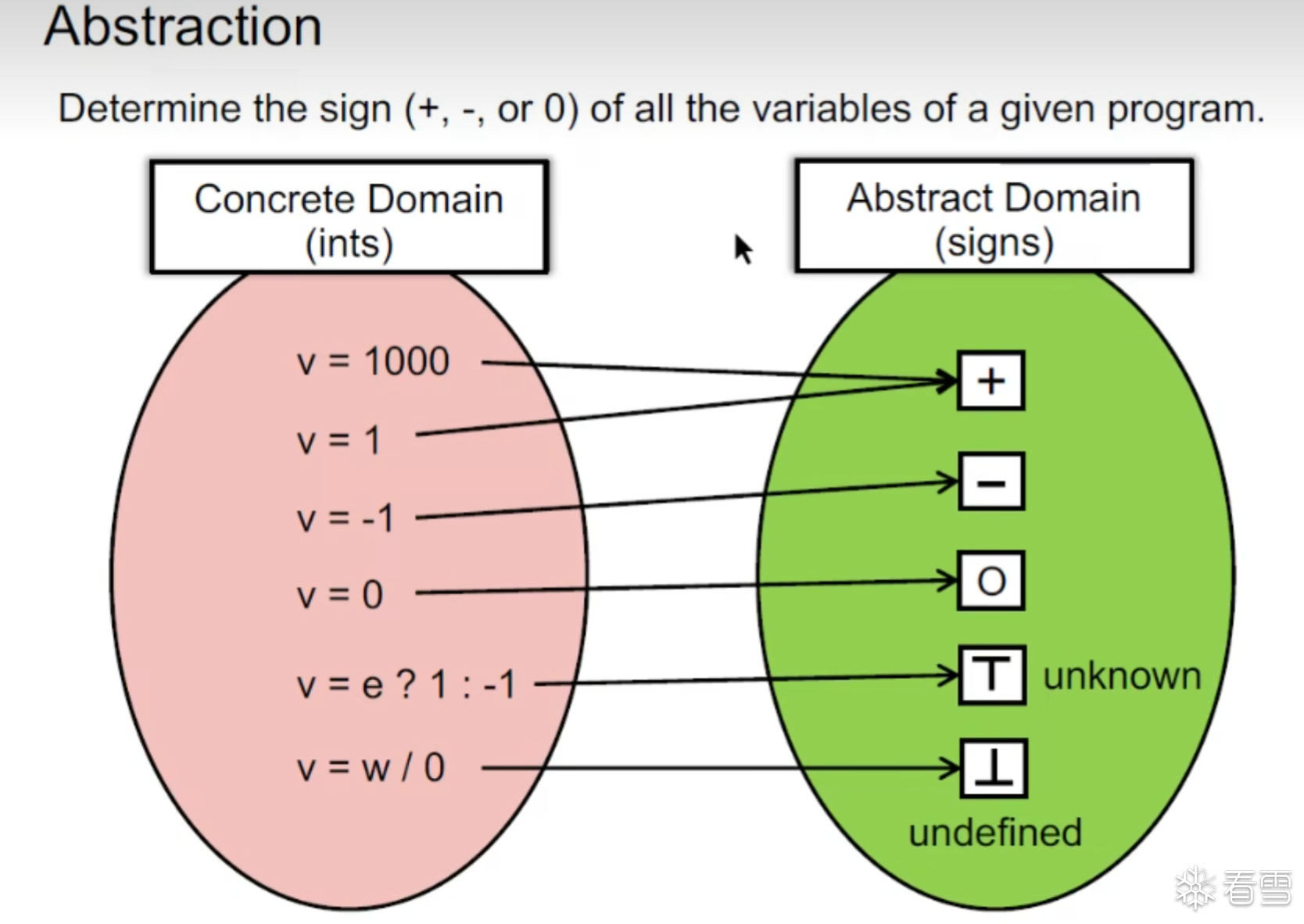
即根据语义进行抽象出的符号后构建的转换函数。如下
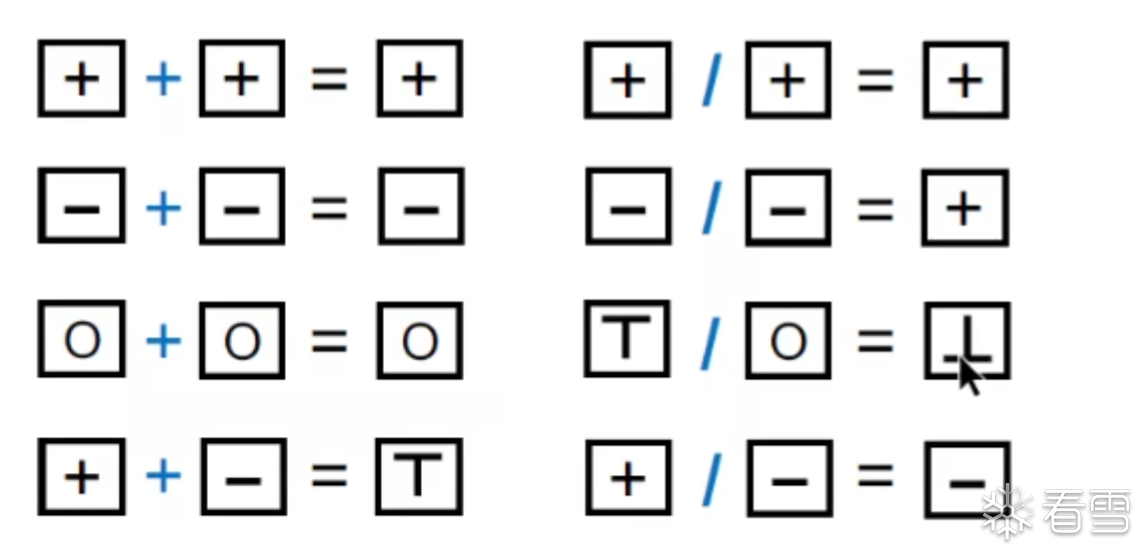
然后根据这些规则我们可以进行推断
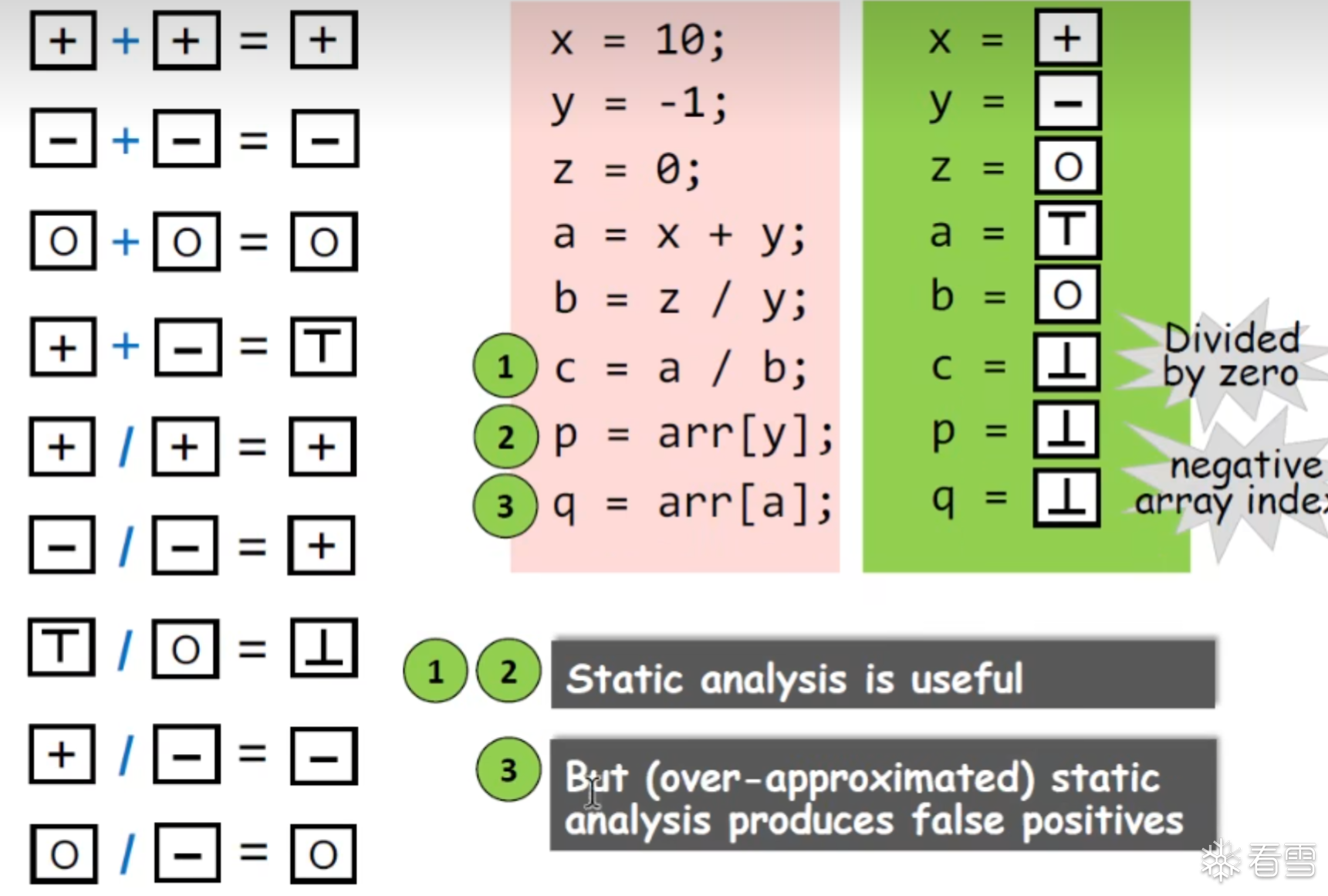
近似的控制流抽象
在所有节点合并的时候我们必须对该节点进行flow merge
对于程序分析来讲我们都是通过IR去进行分析的。
对于编程语言来说context free gramma 已经足够了，整个编译流程
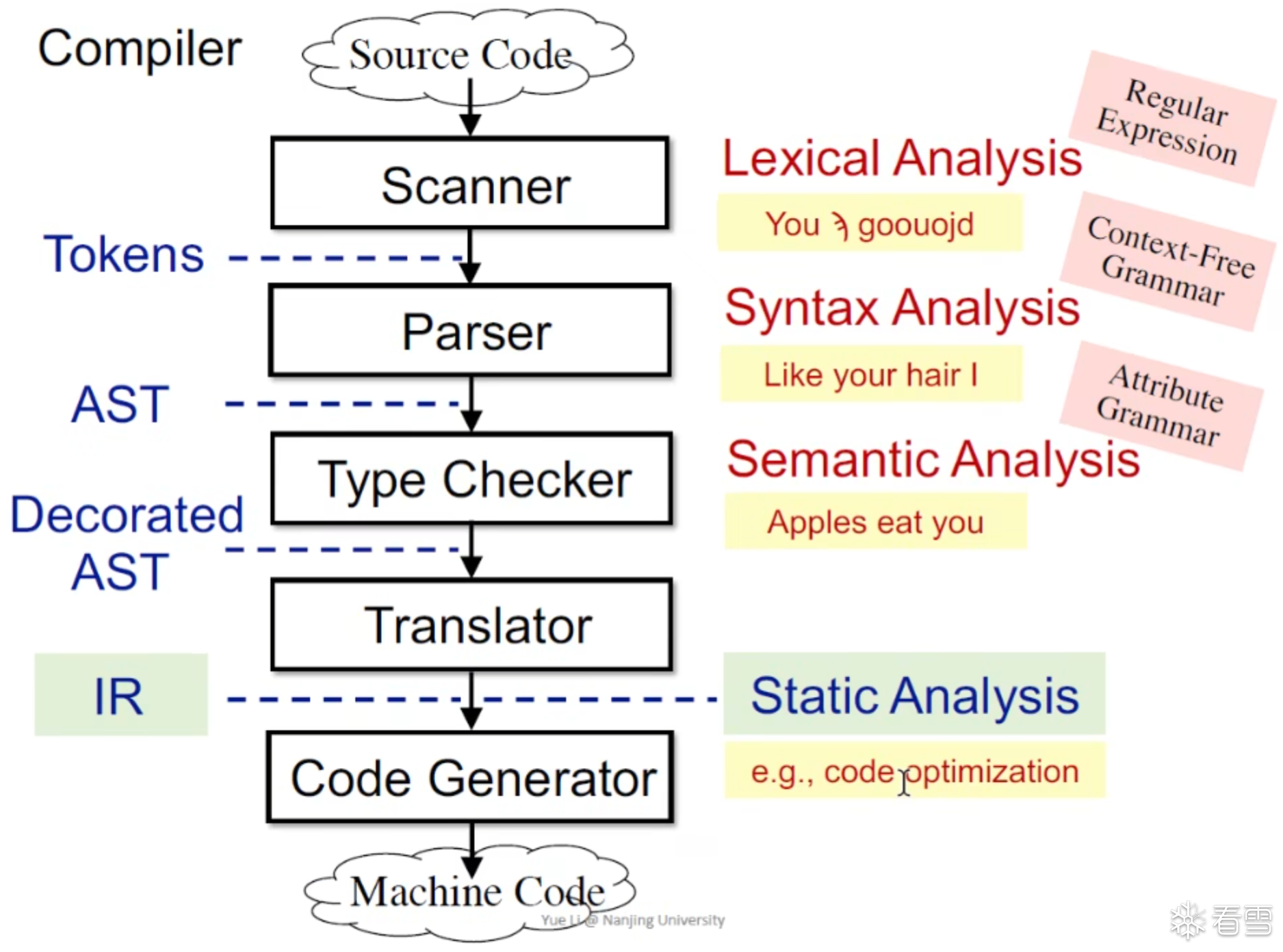
对于3地址码是更利于静态分析器的因为3AC是包含有控制流信息的，而常规AST仅仅适用于进行快速的类型检查。
在3AC中我们可以接受如下3种类型
最流行的静态分析器
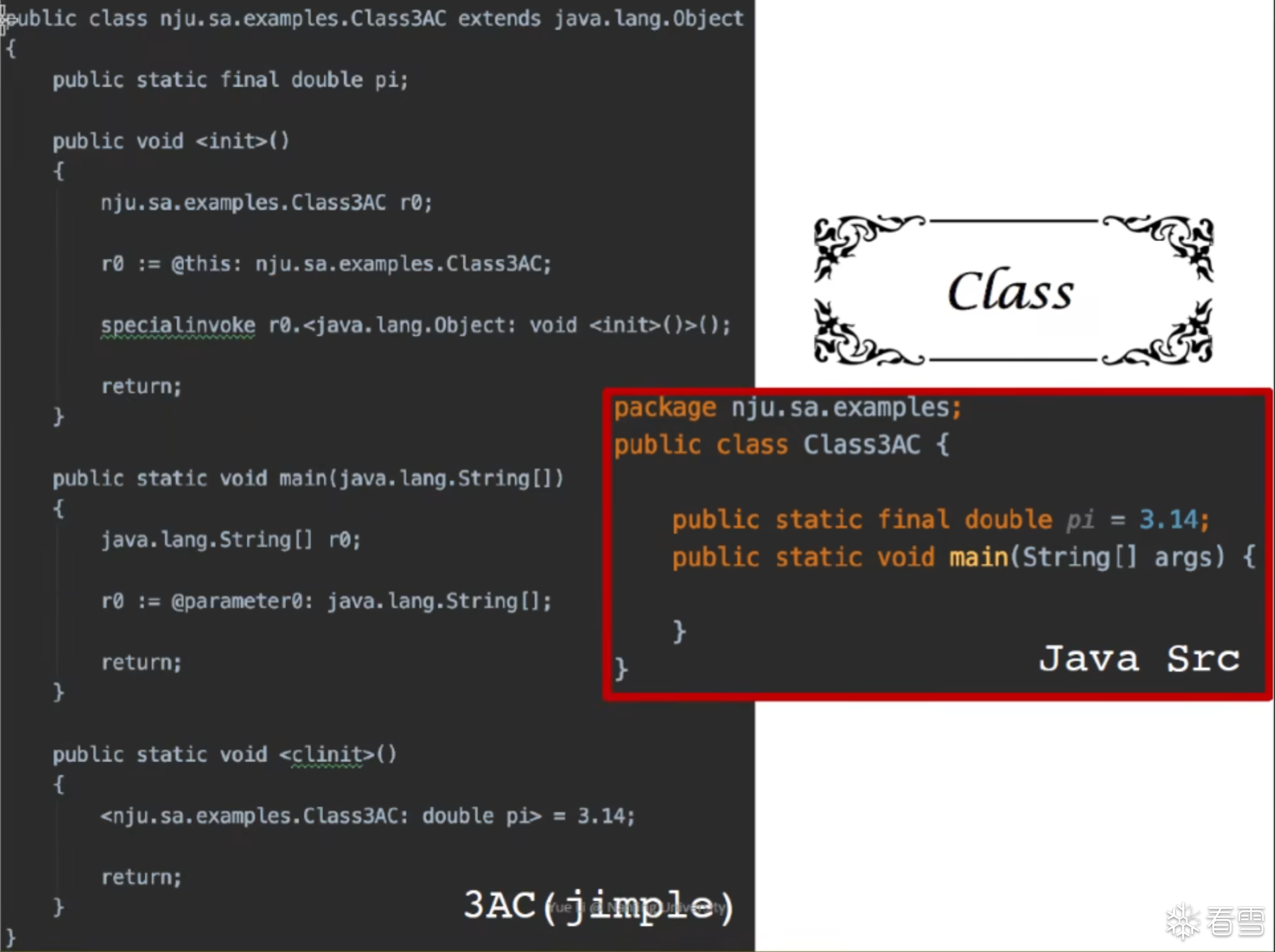
Soot的IR是 Jimple 是一个带有类型的3地址码: typed 3-address code
Jimple 3AC
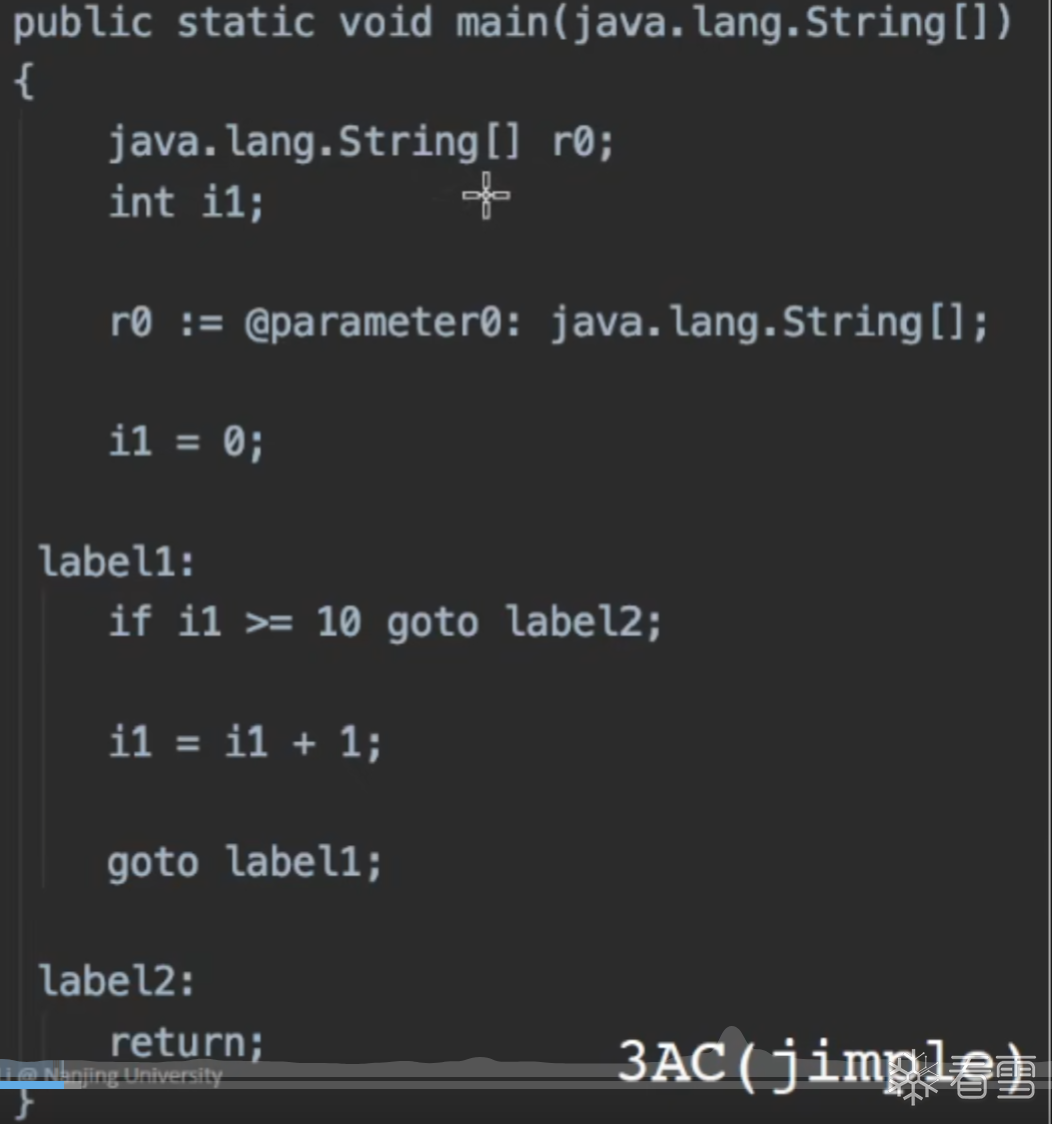
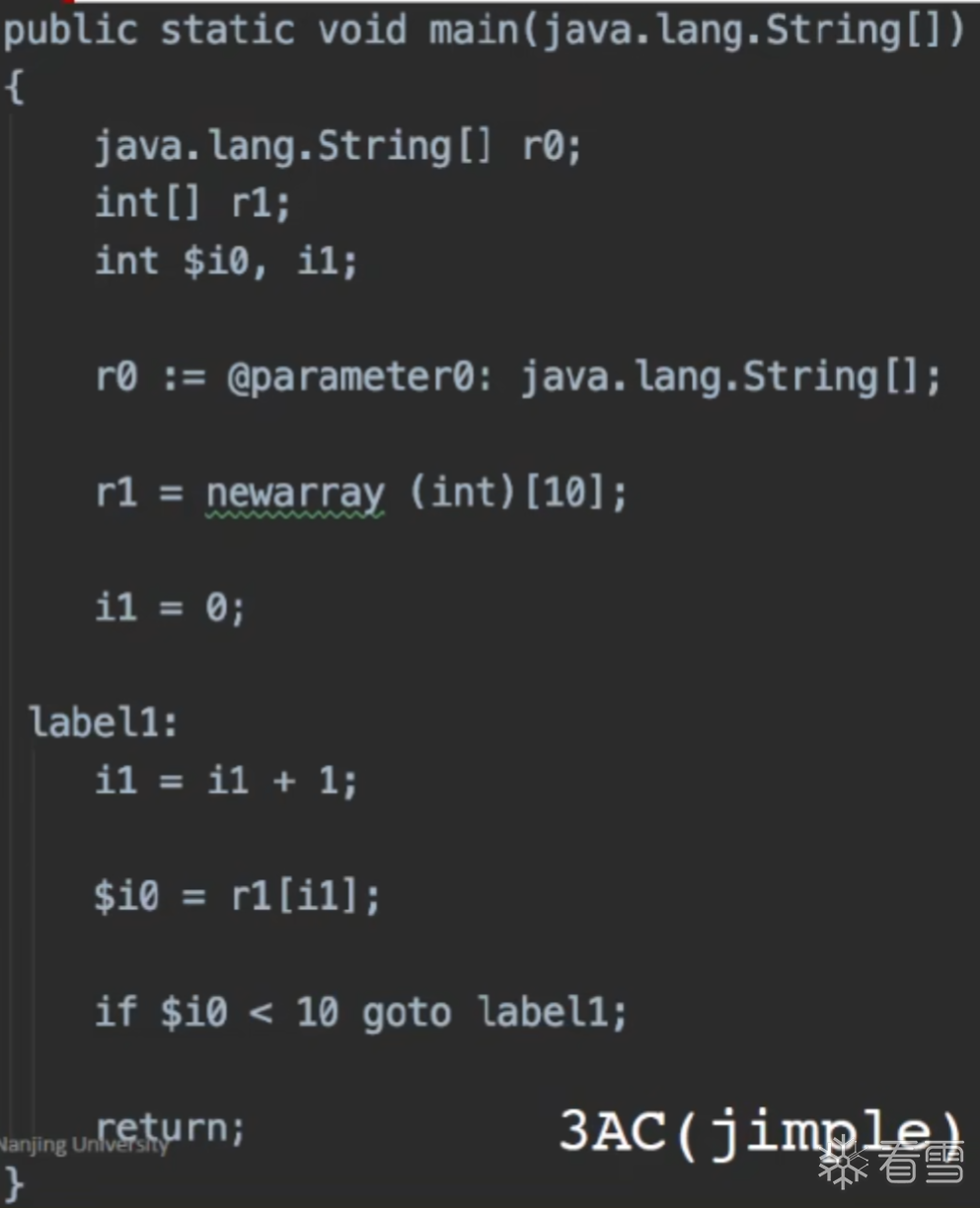
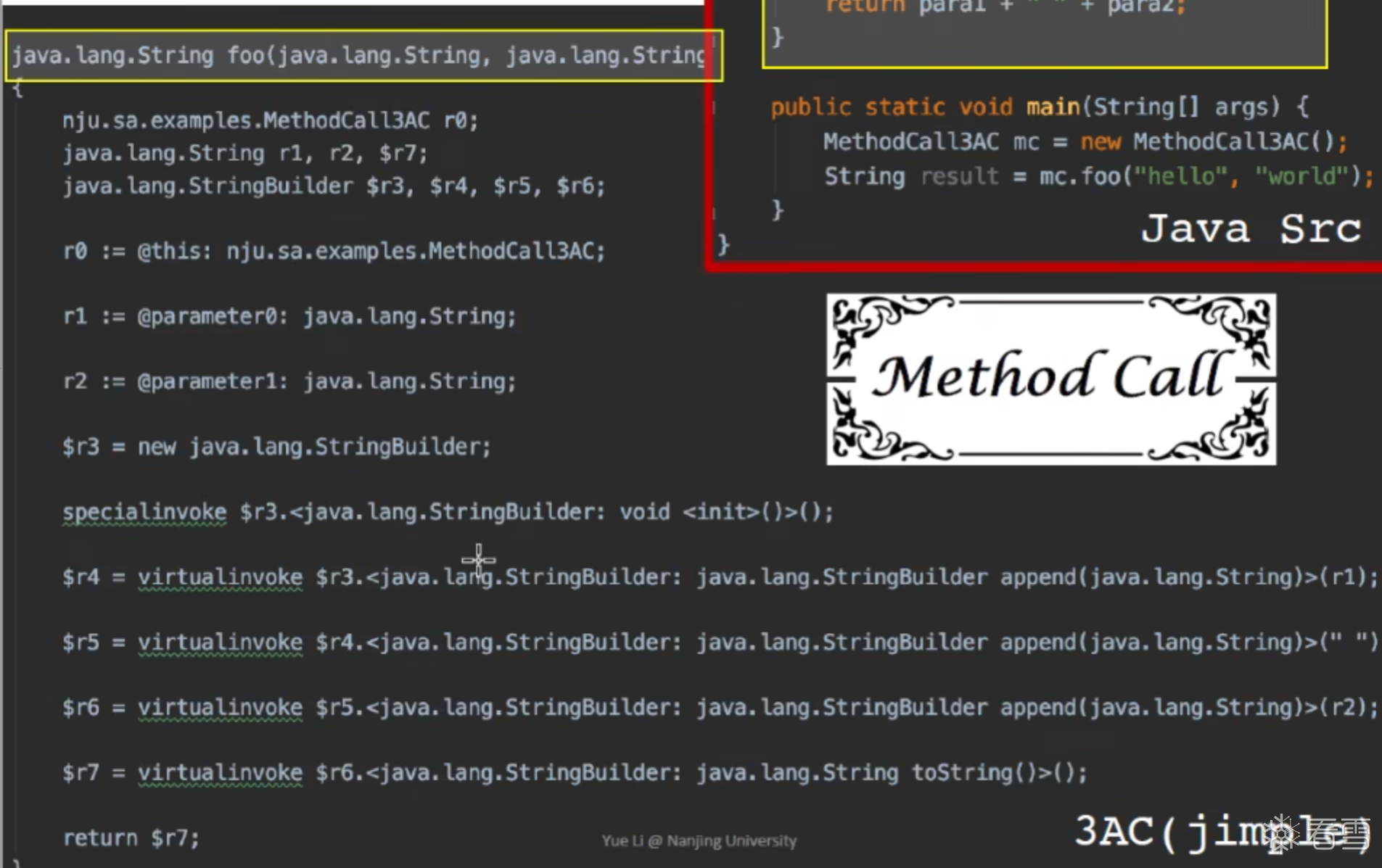
其中尖括号里面的东西是 method signature: class name: return type method name(parameter1 type, ...)
这个就是之前学过的方法签名。
JAVA中常用的 INVOKE类型
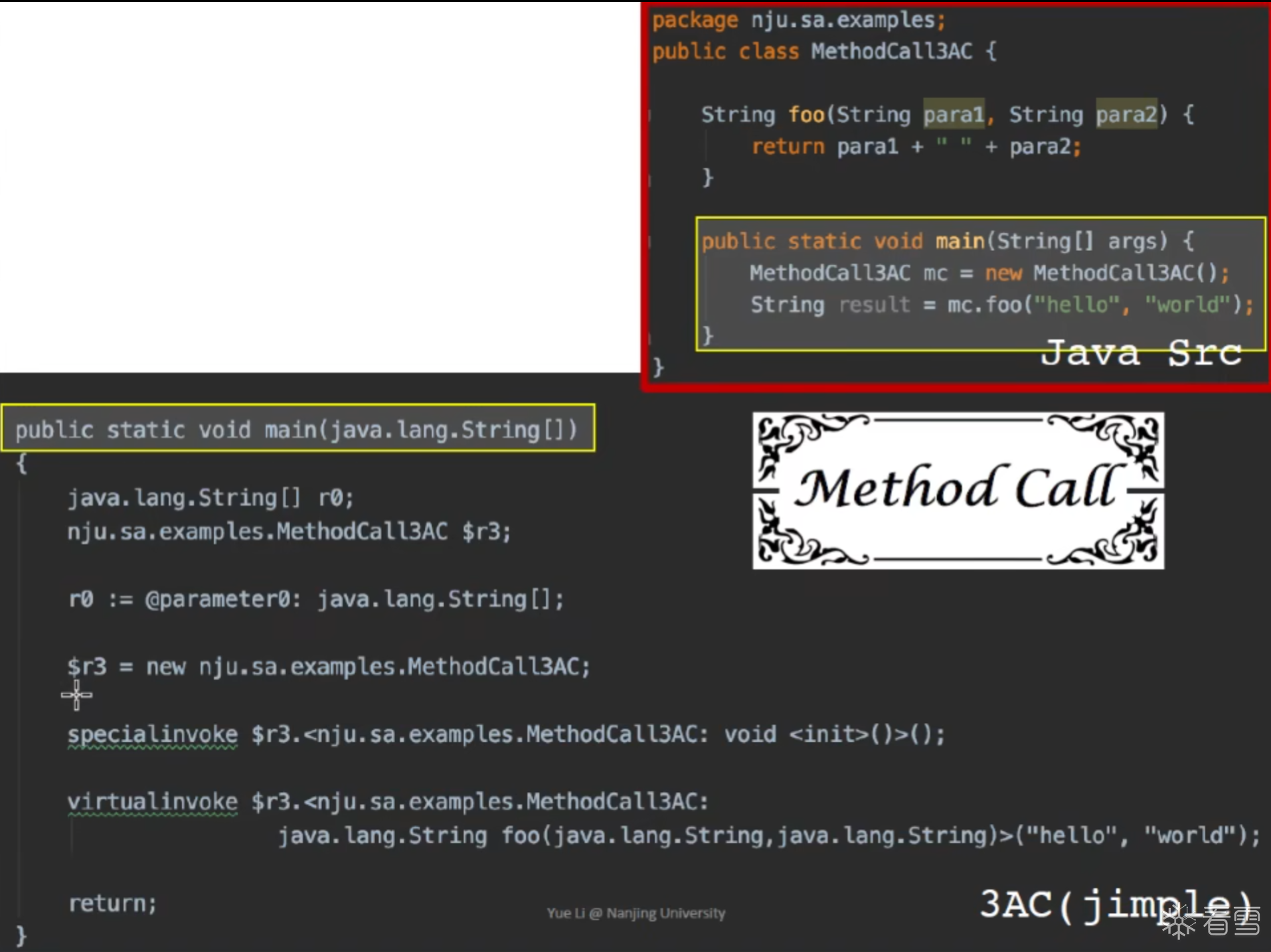
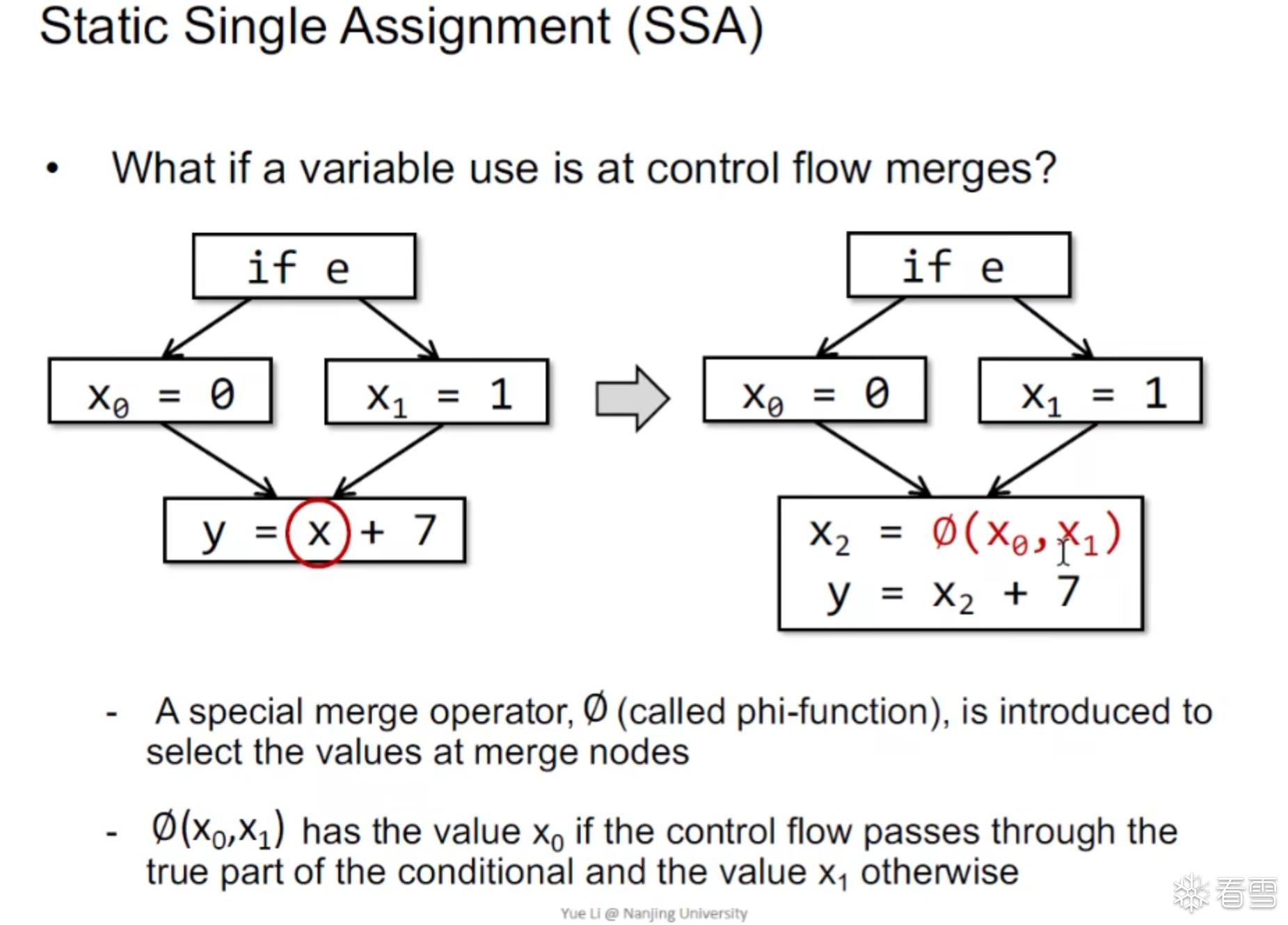
对于PHI 函数主要对于 多个基本块汇合的时候根据特定分支的值选取对应变量的值。
我们需要通过程序的三地址码生成对应的CFG,其中CFG是所有的 静态分析的基础。
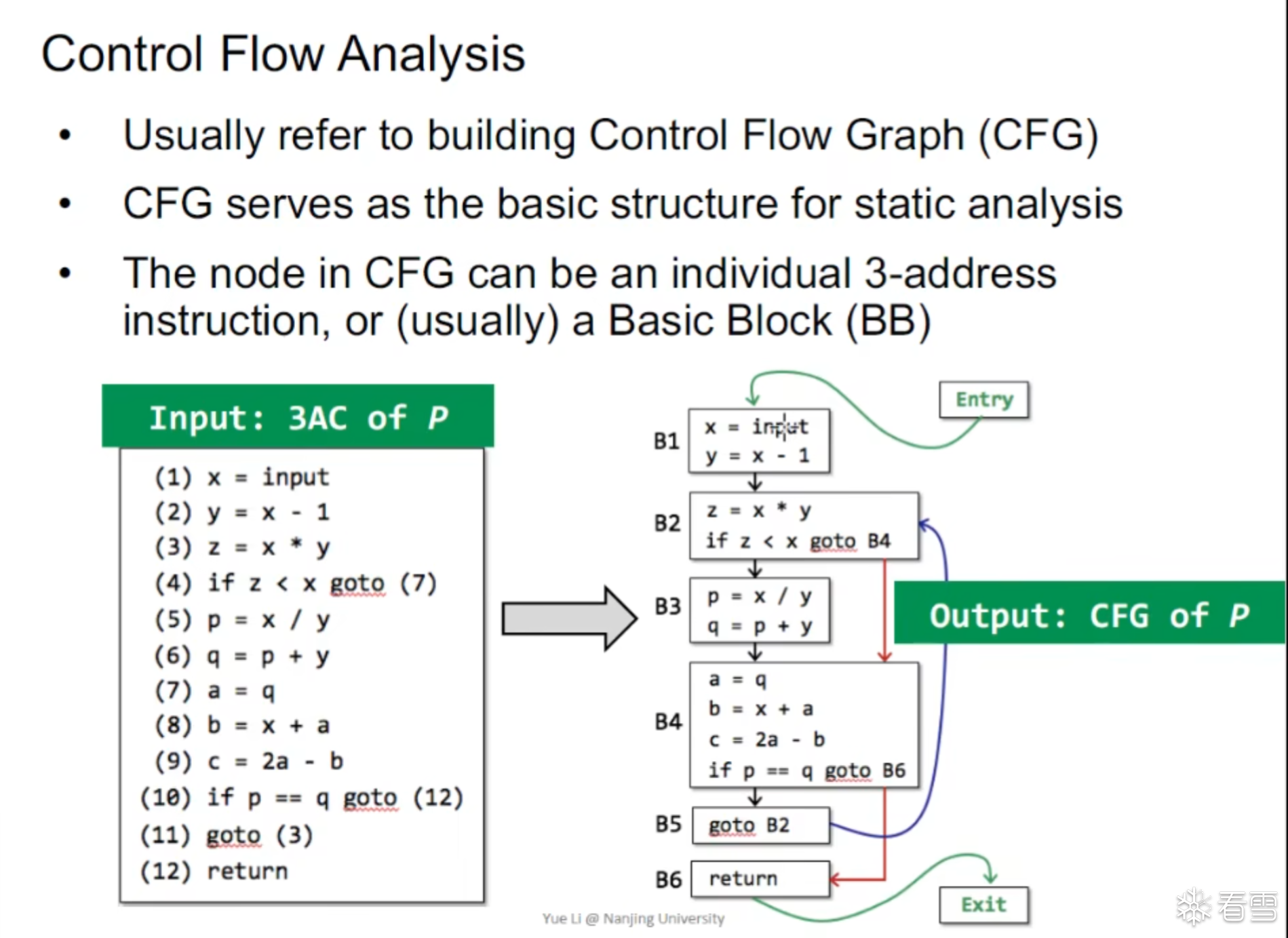
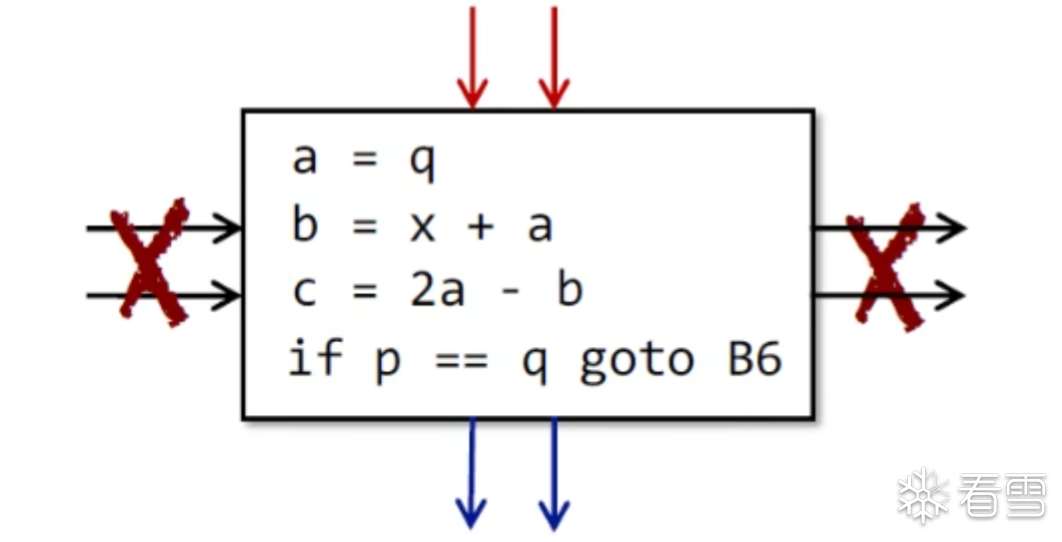
在这里我们并不需要寻找相关的出口而是下一个BB的入口的上一条指令作为结束。
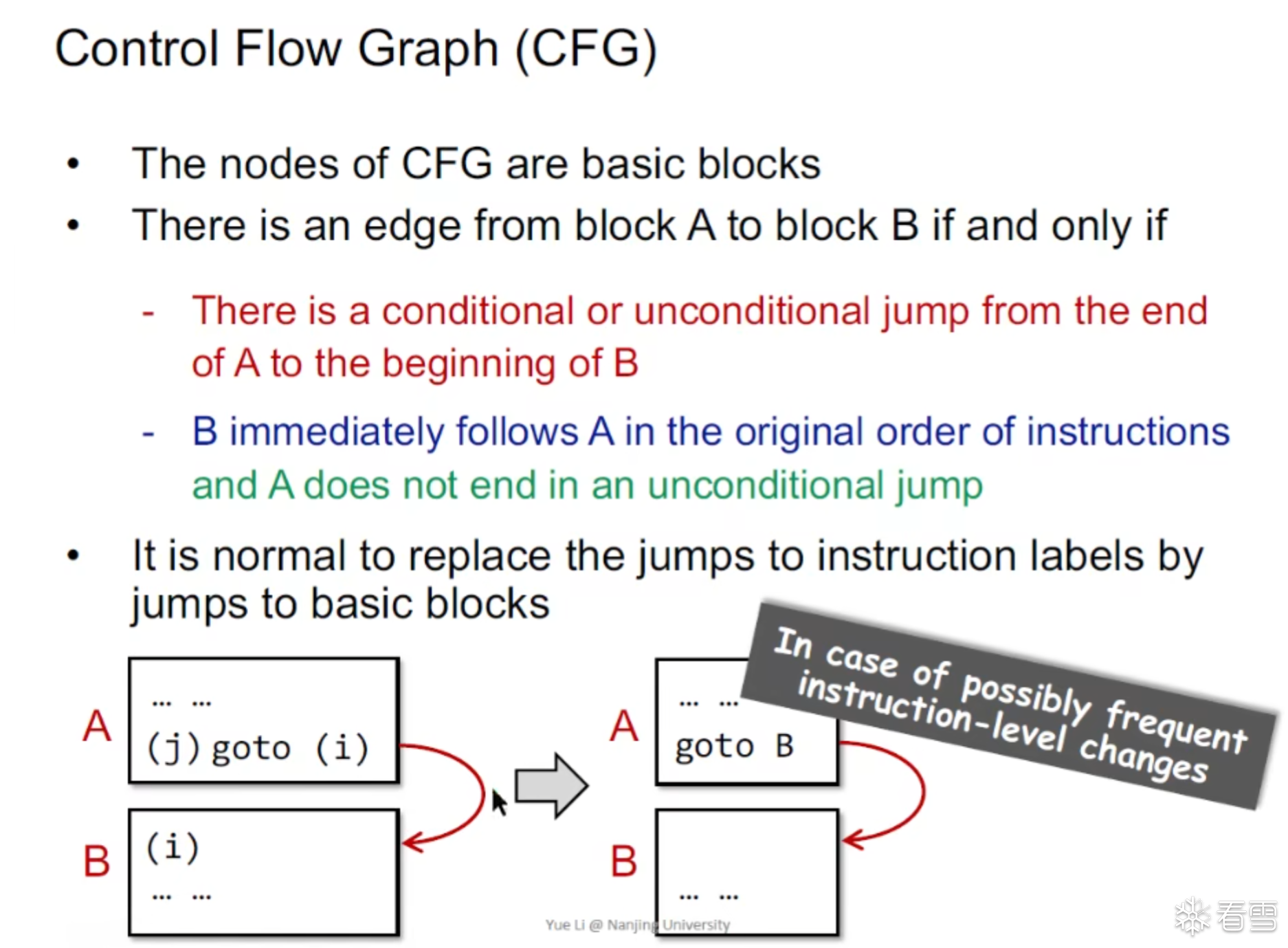
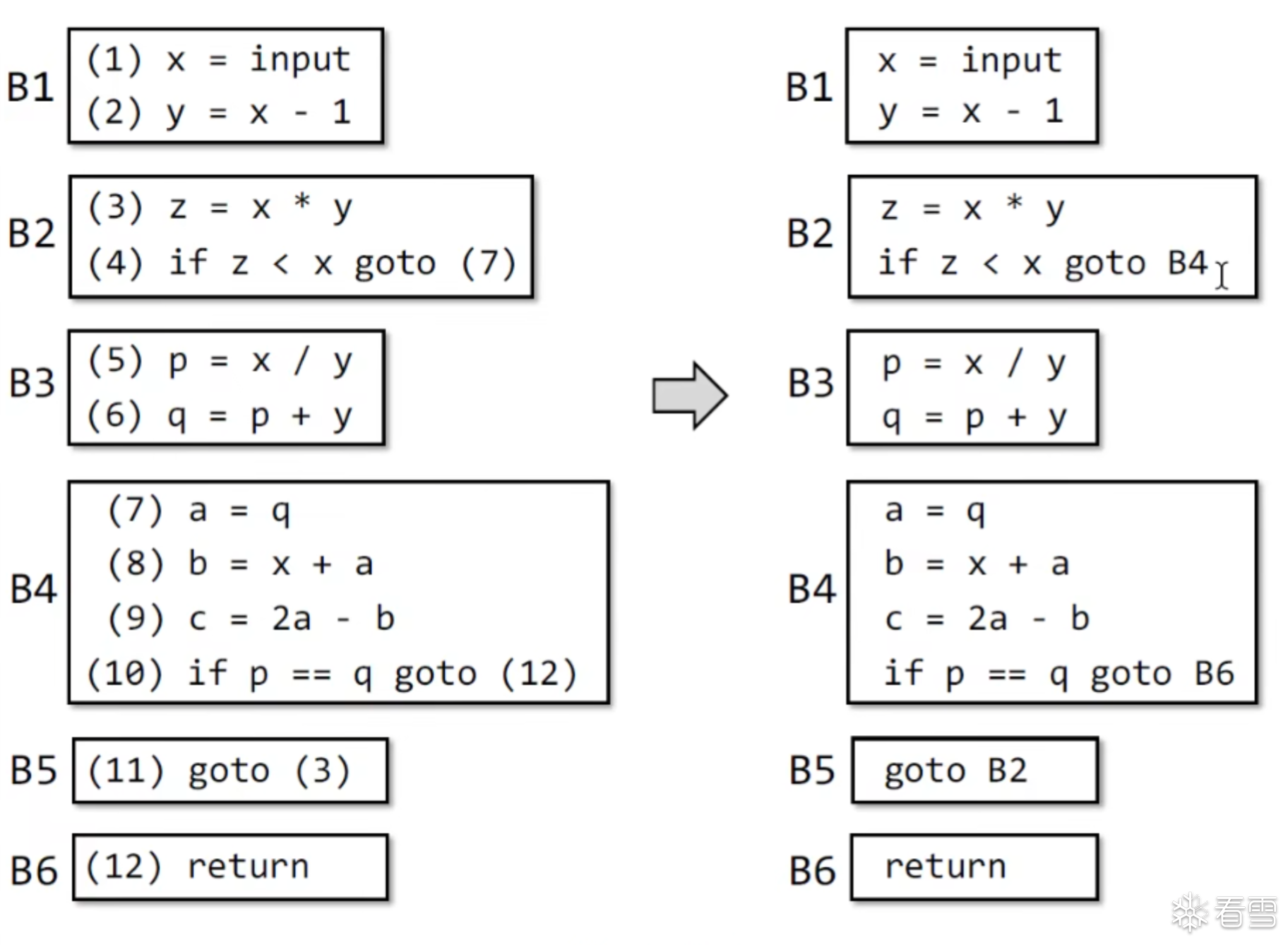
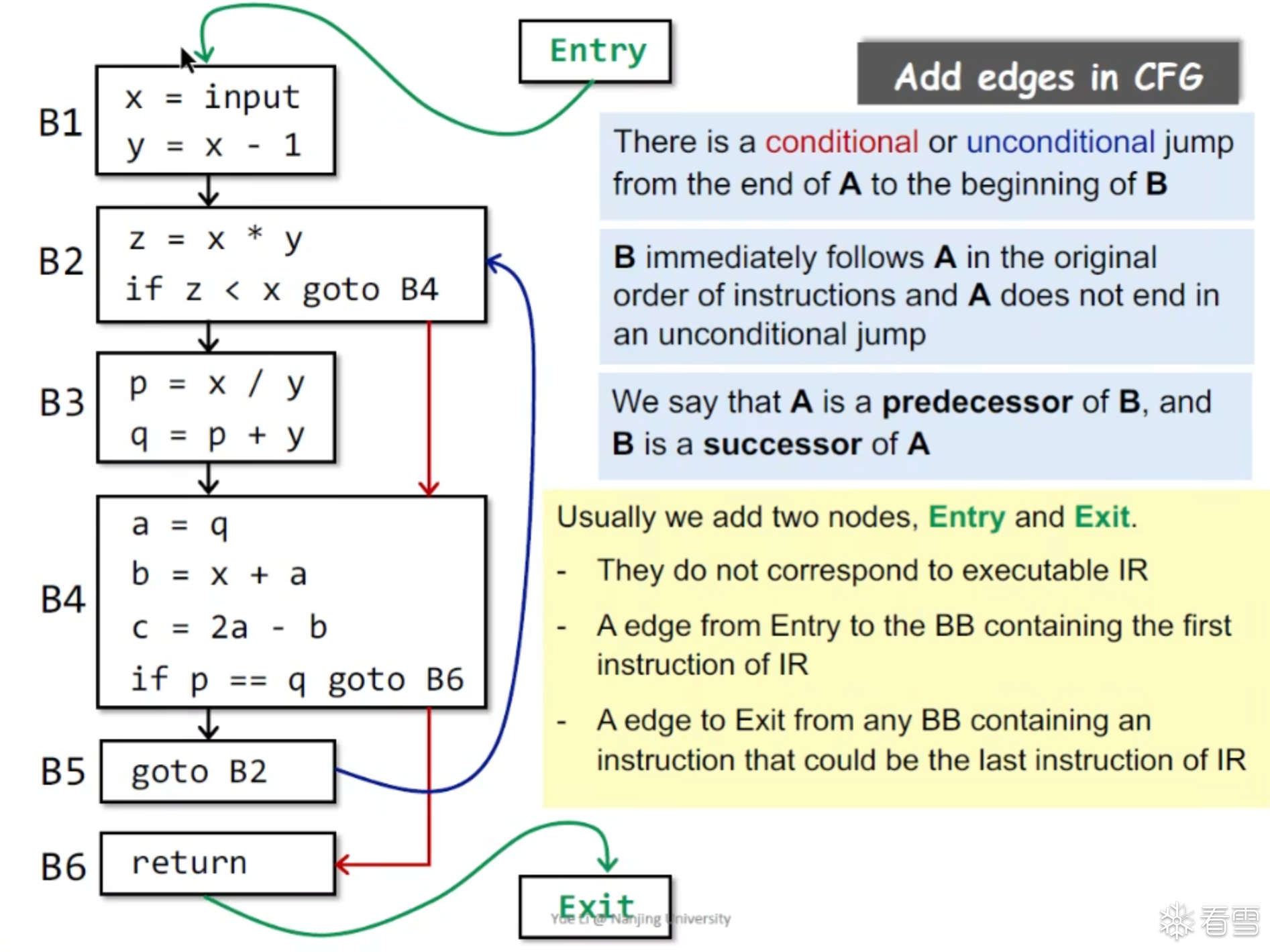
CFG Entry 和 Exit块设置
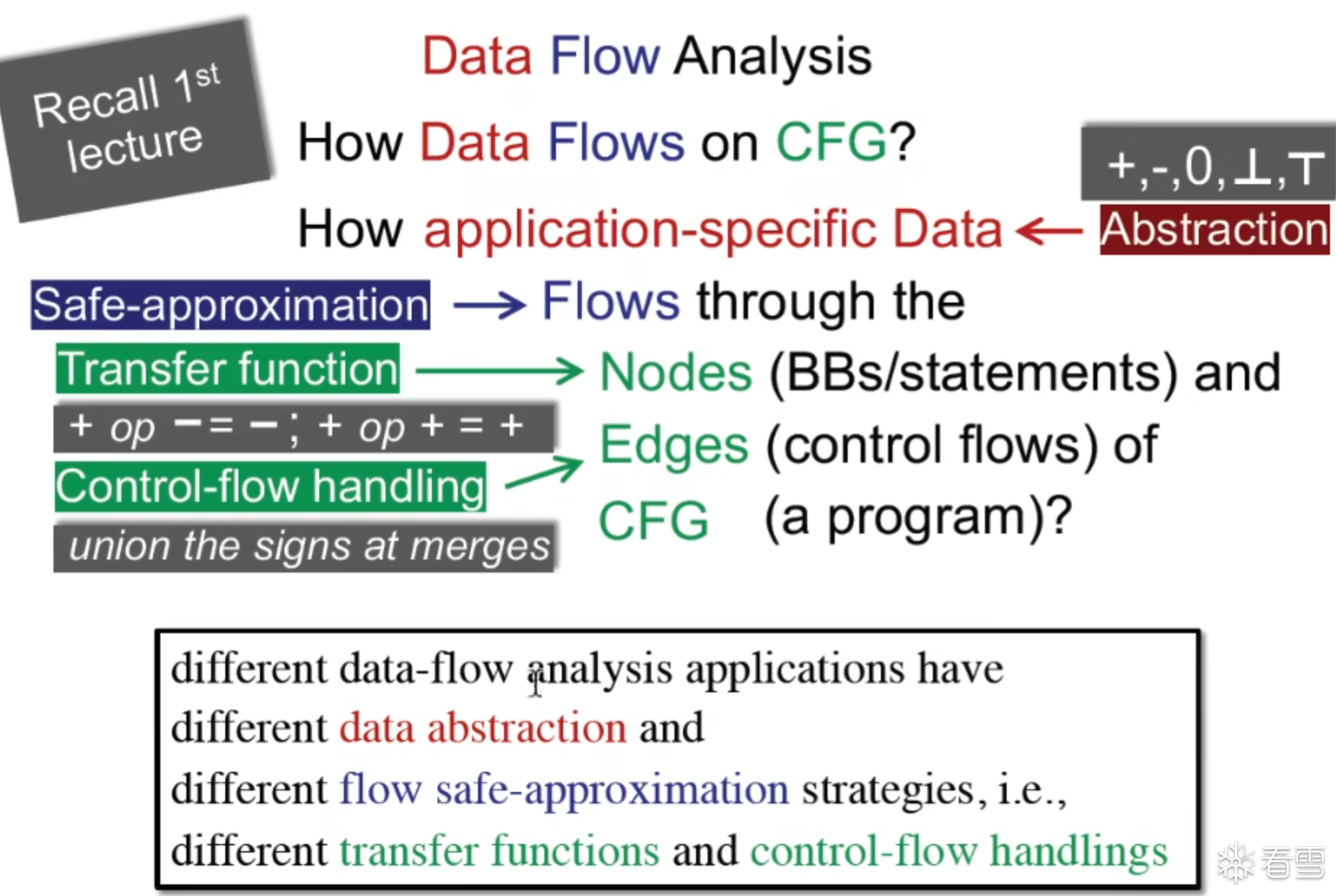
最核心的研究方向 就是数据是如何在CFG上流动的
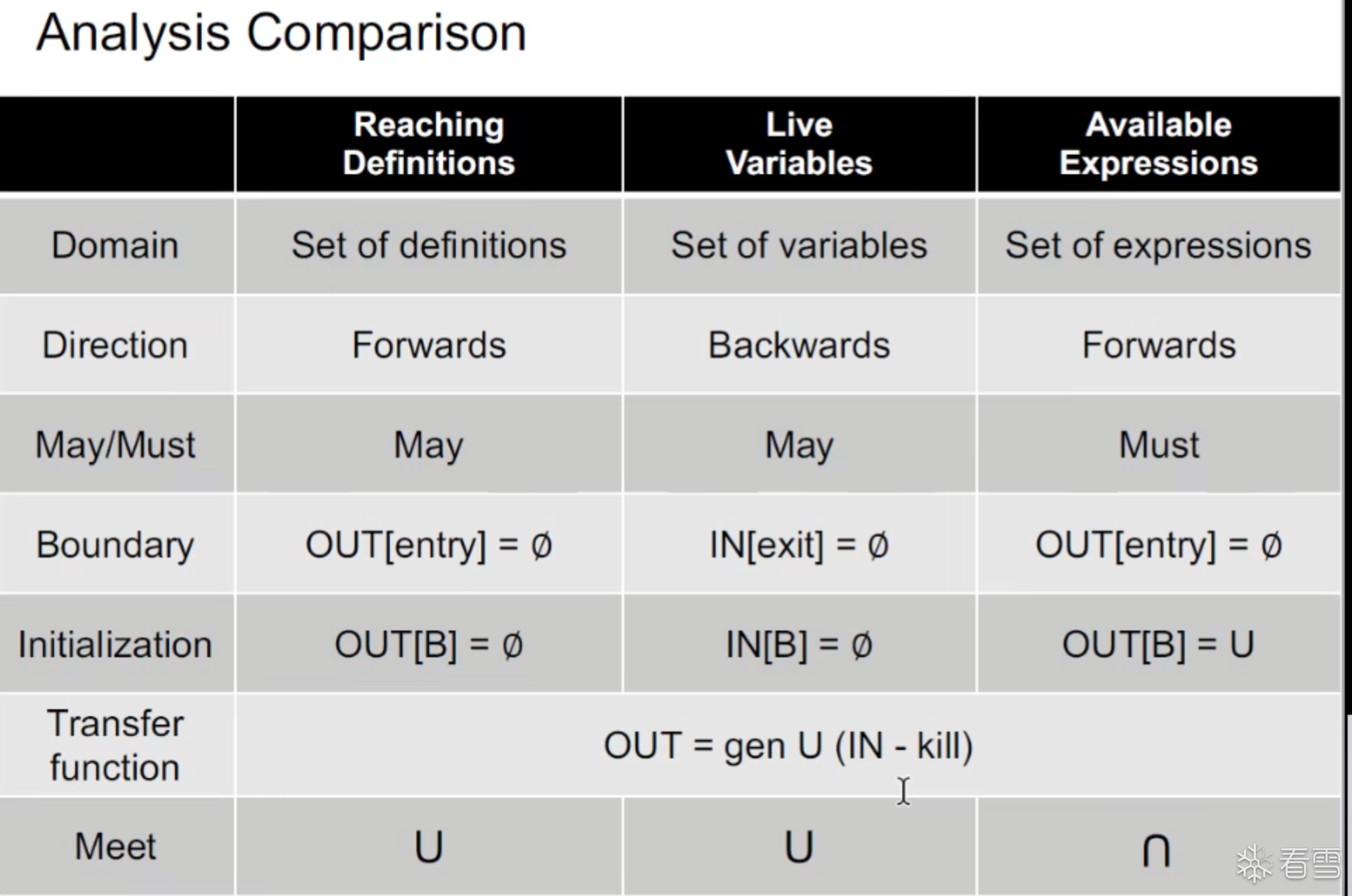
对于静态分析主要有两种分析模式
特性
May Analysis
Must Analysis
中文
可能性分析
必然性分析
语义
"至少一条路径"
"所有路径"
结果
可能多算(保守)
可能少算(激进)
汇合操作
并集 (Union)
交集 (Intersection)
属性
Sound
Complete
控制流分析的4大核心要点
Variable(变量)
Definition(定义)
我们可以用IN[s1] OUT[s1]来表示 输入和输出的程序状态
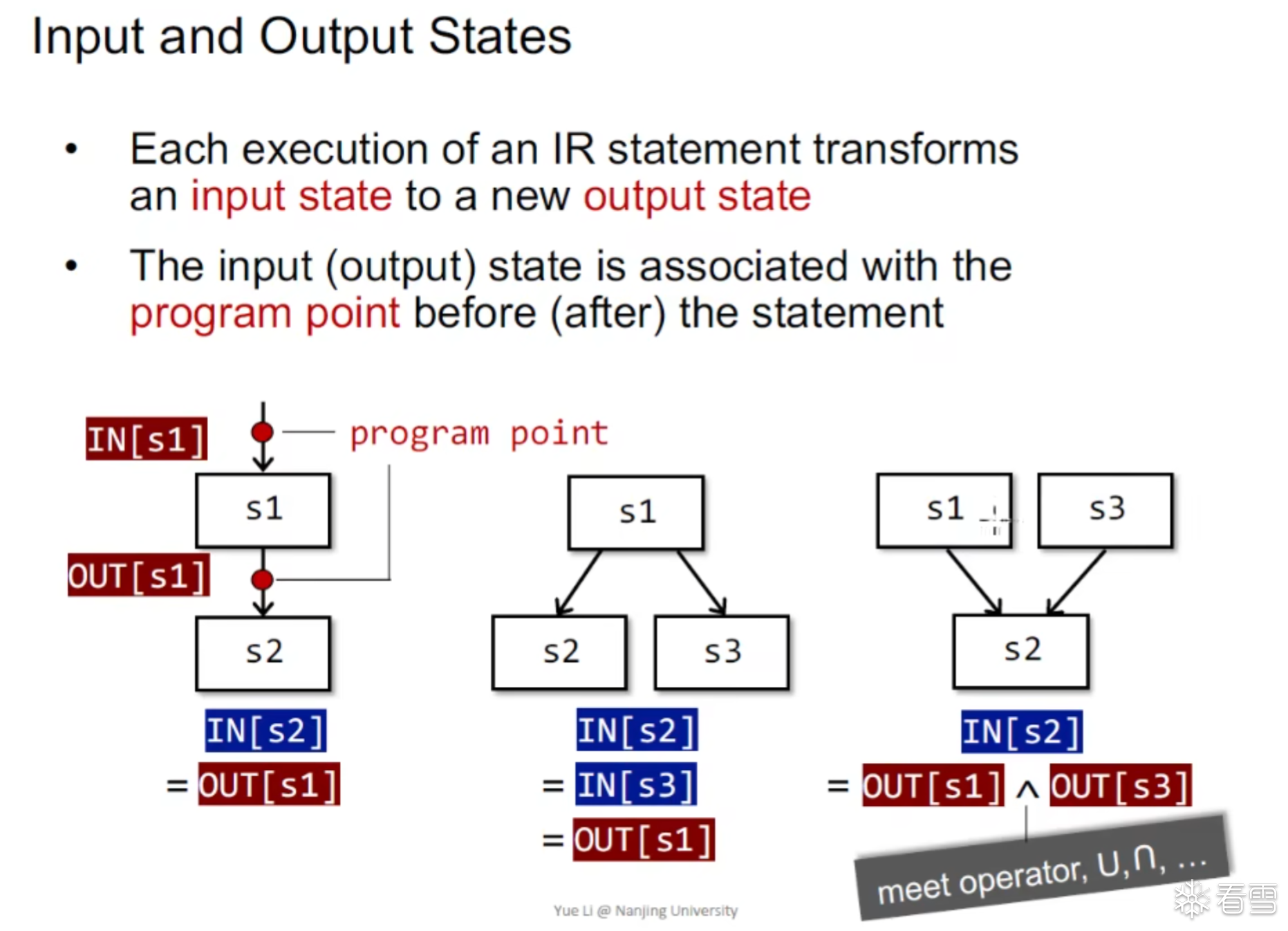
在每一个数据流分析应用中，我们为每一个程序点关联一个数据流值，这个值代表了在该点可观察到的所有可能程序状态的一个抽象集合。
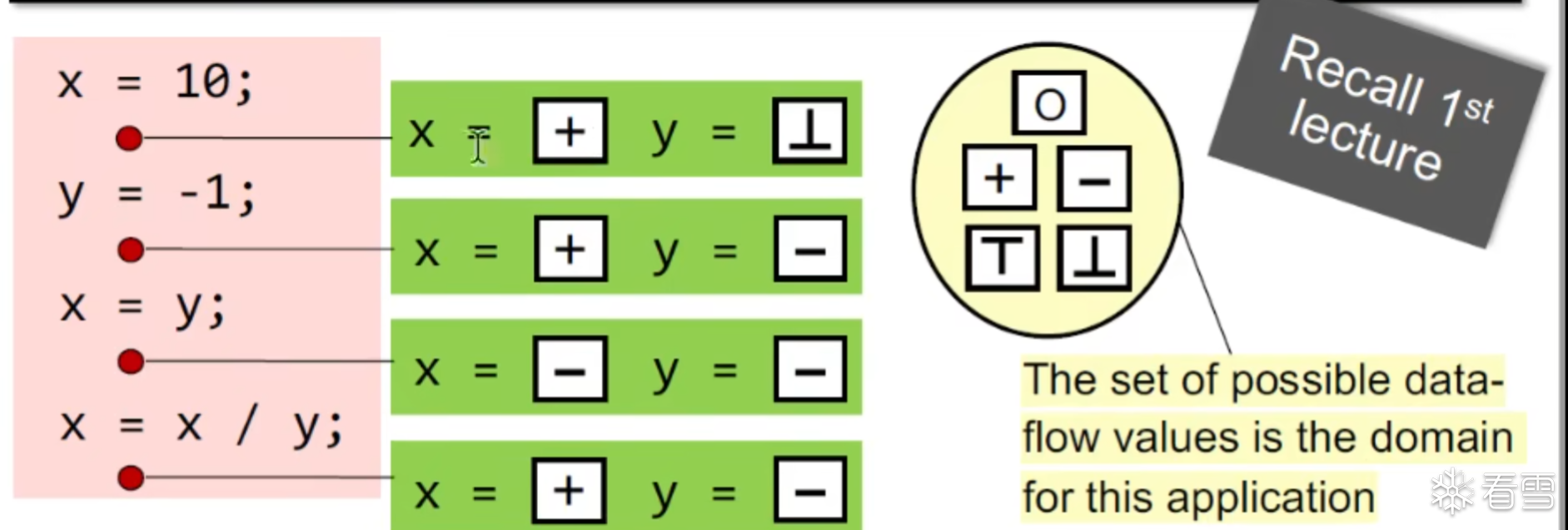
其中绿色为Data flow value 红色的部分的点是抽象的程序点，黄色的是 抽象符号的值域
从另一角度来说 数据流分析 就是通过 解 安全近似 在 IN[s]和OUT[s]的约束规则该约束规则作用于全部statements. 我们不断的解转换函数和控制流信息的约束规则就能得到一个解，这个解就会给每个程序点标记上抽象的flow的值
两种转换函数的约束形式
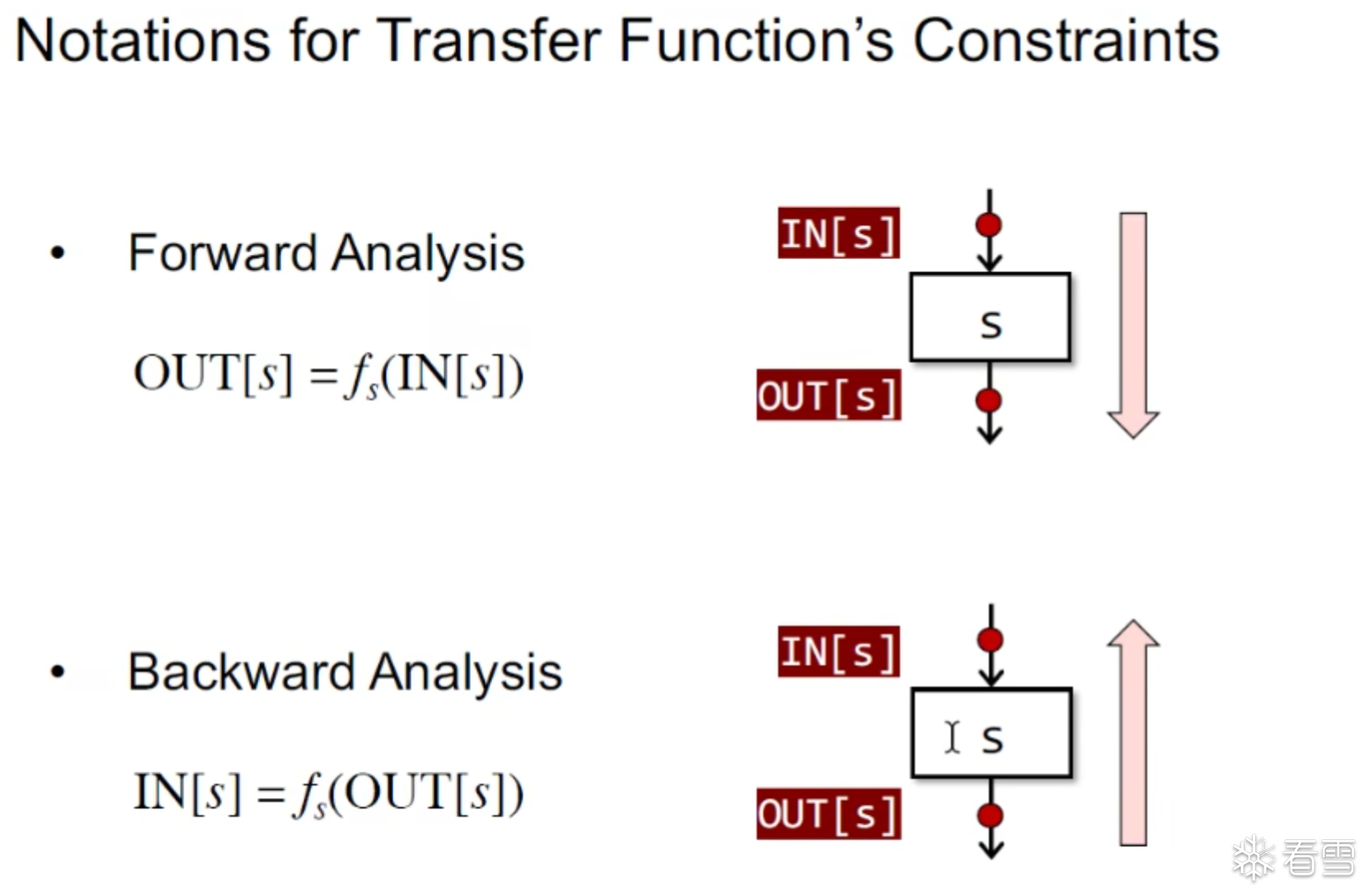
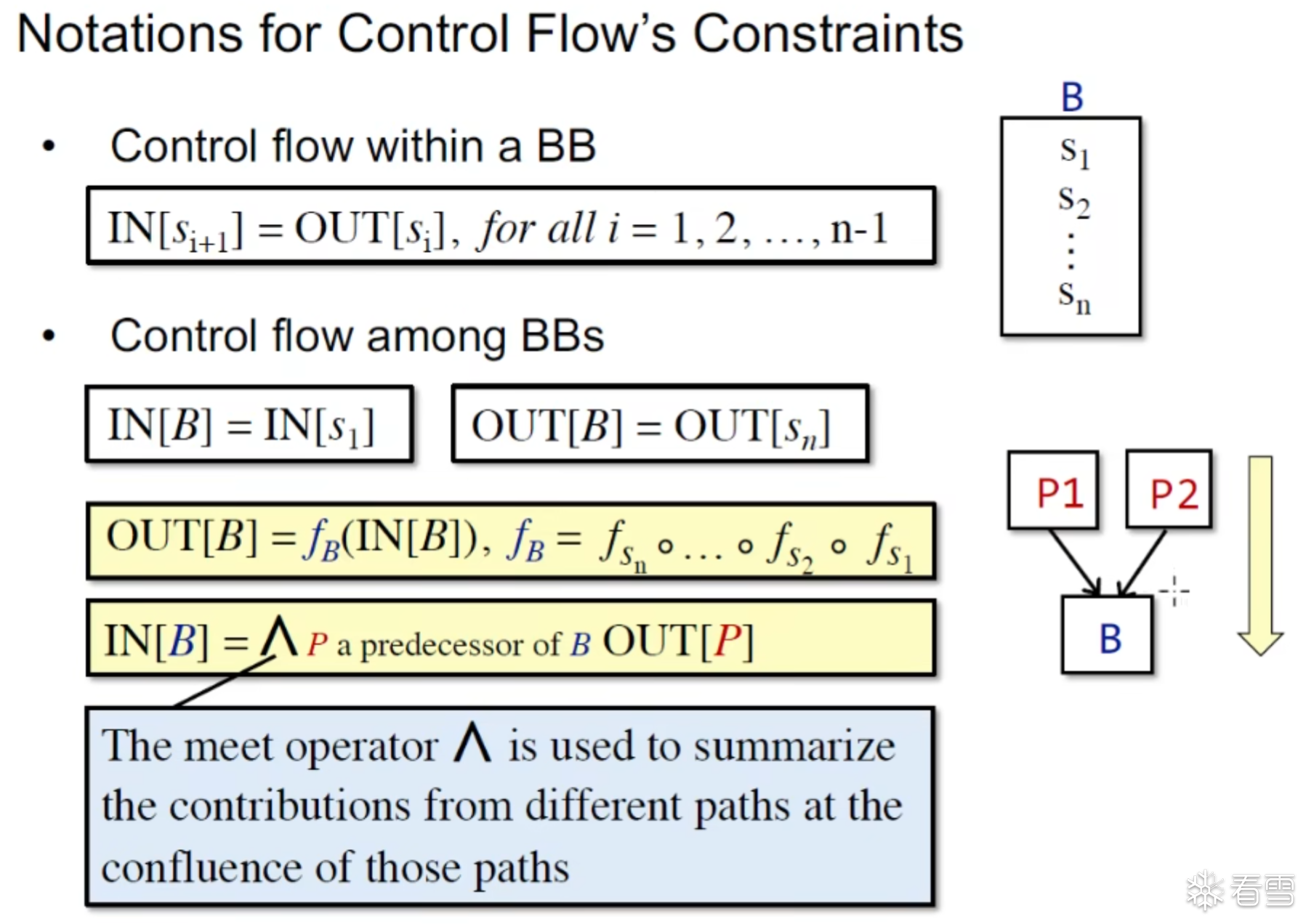
对于汇聚结构的B输入是由B的前驱^OUT[P],反向分析
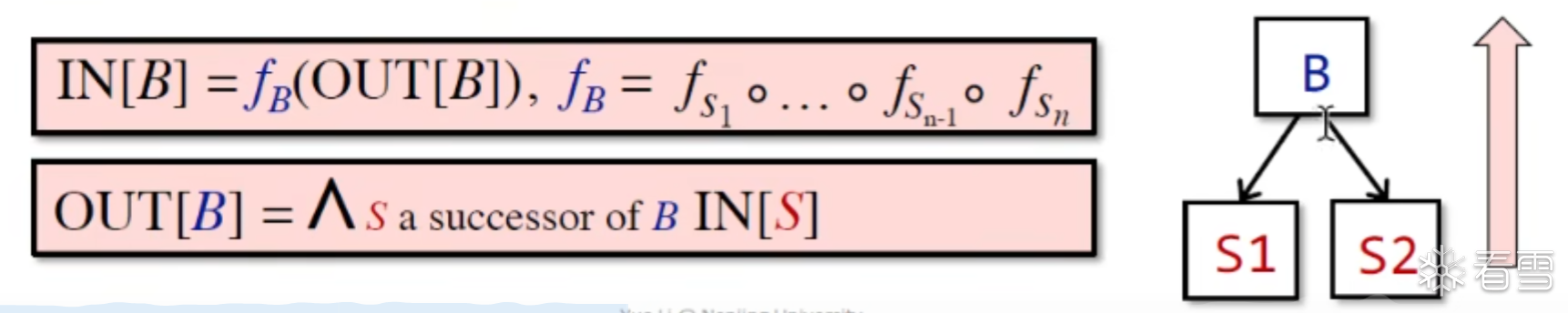
目前还没有触达的问题
对于可达性分析的这里的分析类别应该是 may-analysis， 比如在程序中有100条path 其中有一条是没有初始化的path 我们应该用over-appro 去进行近似以便于将其归纳到报错当中去。
对于我们常见的分析情况我们在 Entry BB处对每一个变量给出一个Undefine的定义
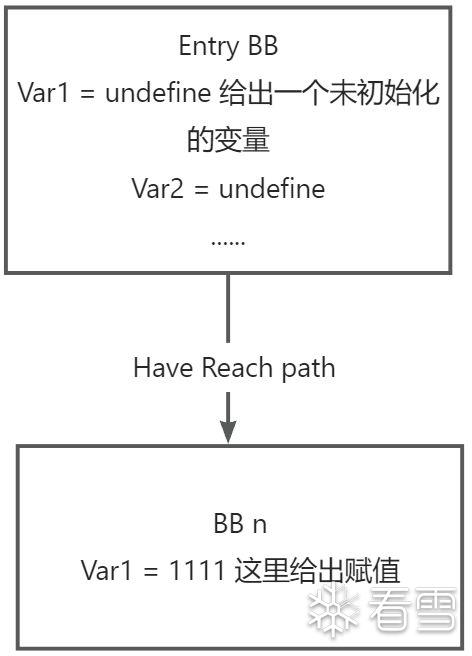
此时我们可以通过可达性分析的解获取到从EntryBB 出发有一条约束路径链接的 n号 BB存在一个 未初始化。这便是可达性分析的一个具体的例子。
对于可达性分析的建模我们同样遵循上面的规则
只要存在一条可达的程序路径就定义一个 程序点。
经典迭代算法模板
初始化 OUT[B] = phi 对于May Analysis 一般为空 ， must Analysis 一般是 Top
例子
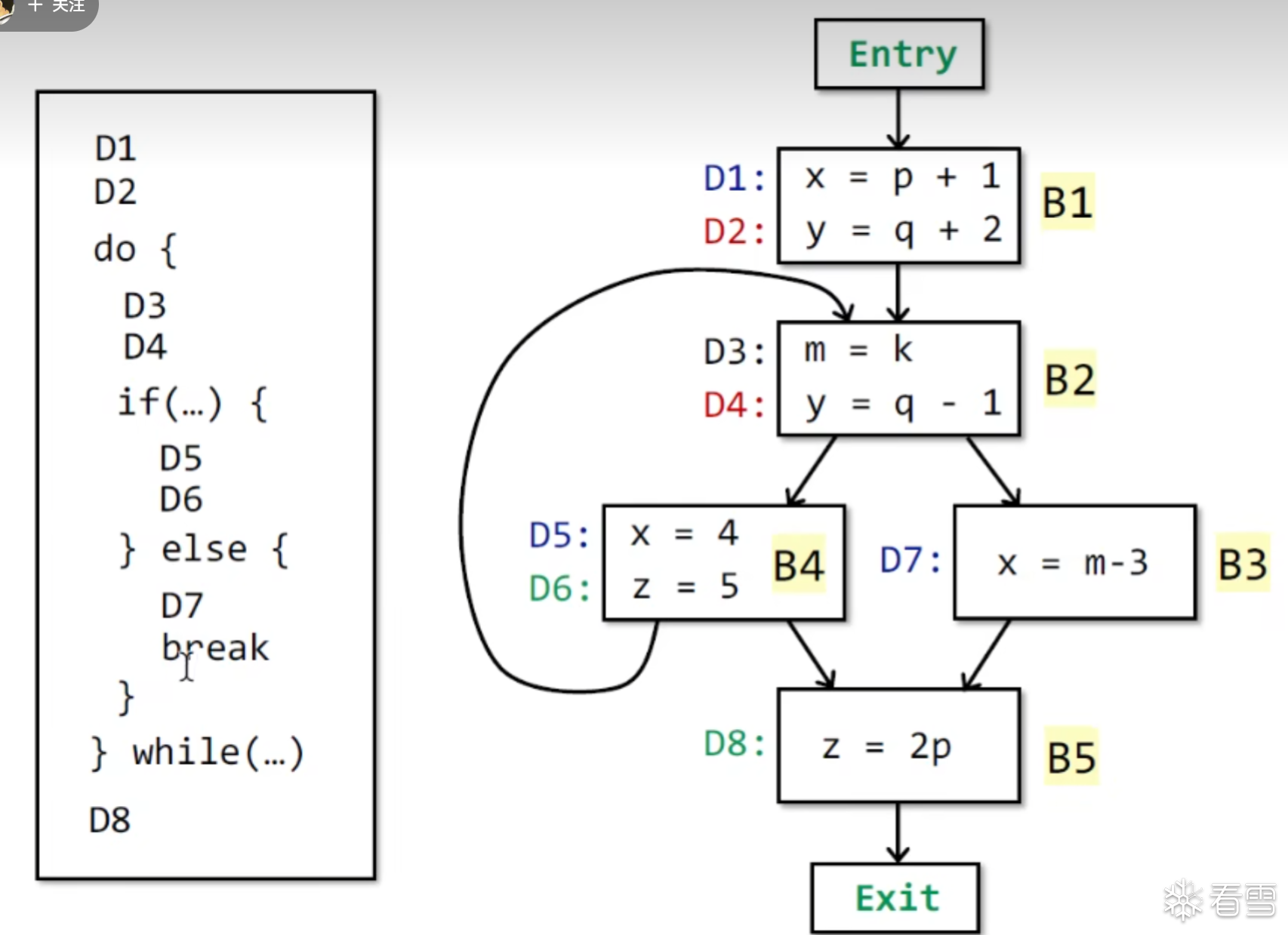
答案:
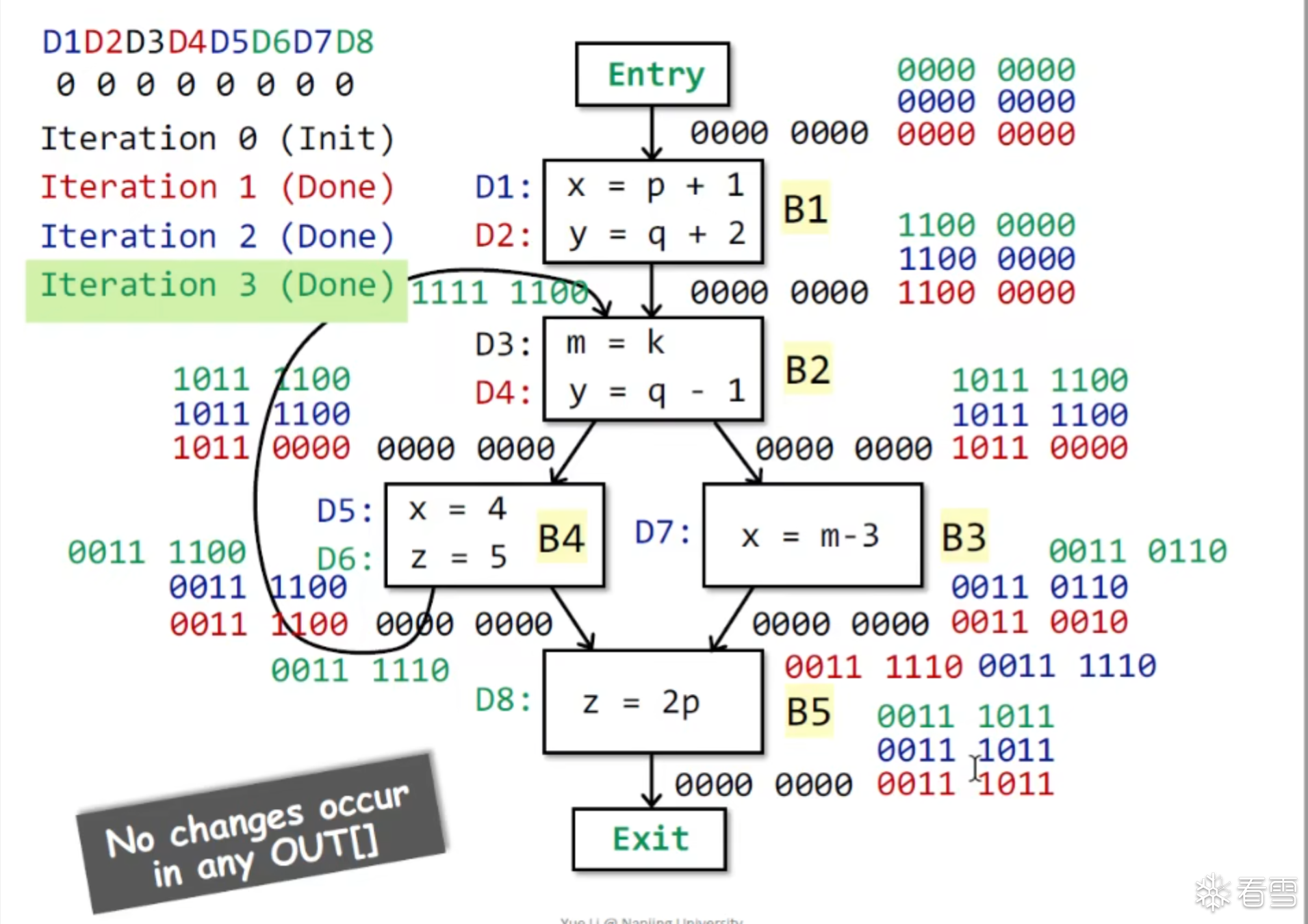
这个迭代算法为什么能停下？
活变量分析是可以让我们知道在P中一点 的一个变量v是否能够在P该点之后进行使用，如果可以则证明该变量是活变量否则为死变量。
可以将这个技术用在寄存器分配上，当我们的寄存器满了之后就可以替换一个死变量，从而不浪费资源。
对于活变量分析的数据抽象我们采用如下方案
对于存活变量分析Backward 分析会更加直观方便。may-analysis，可以设置如下的公式
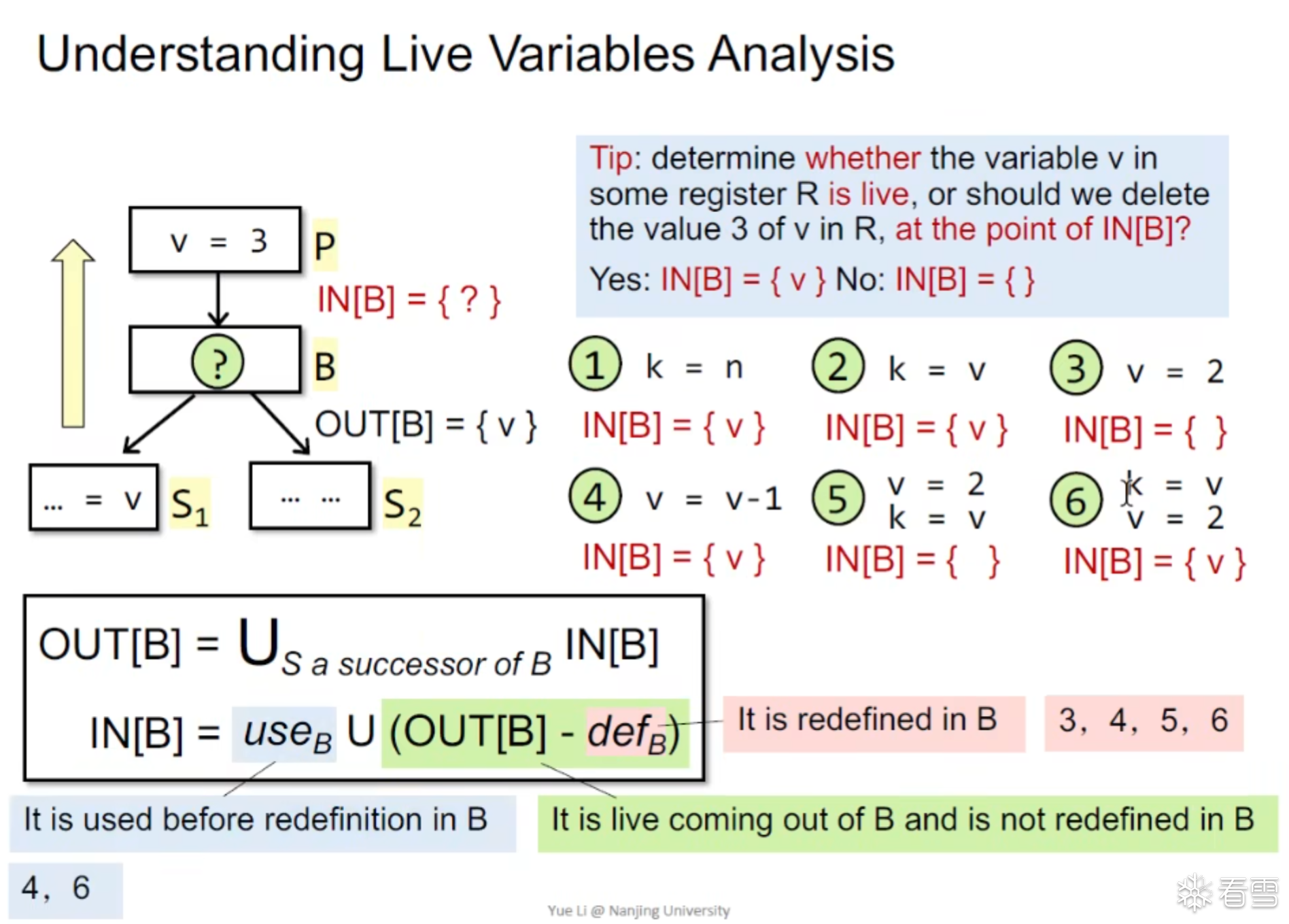
算法模板设计如下
例题
目的: 找出"哪些表达式已经算过了，而且值没变"
应用: 避免重复计算，提升性能
核心思想
一个表达式 a + b 在程序点 P 可用 (Available) 需要满足：
该分析应该是 must analysis
算法
值得注意的是这里的初始化是ALL，即 数据抽象的值为全1
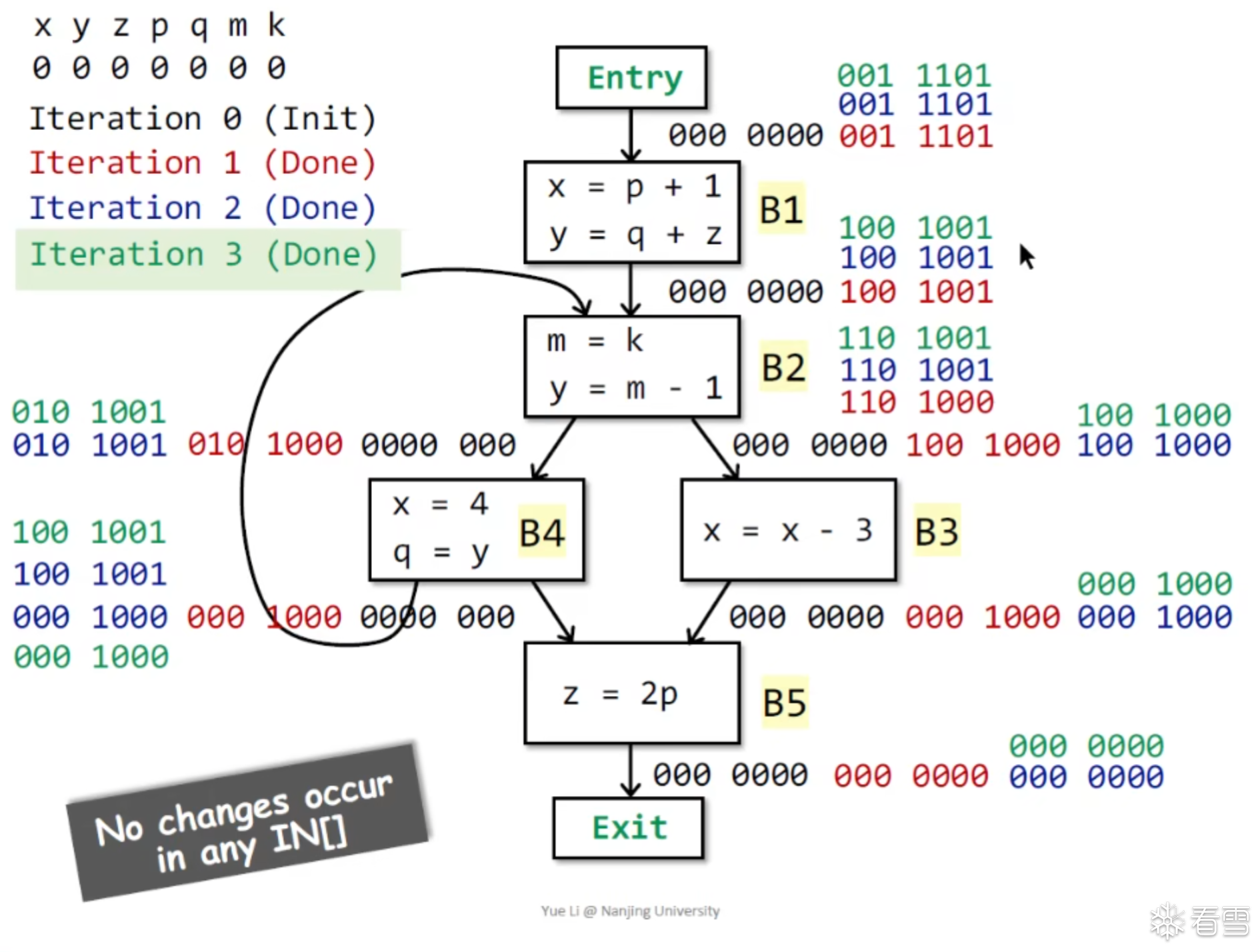
例题
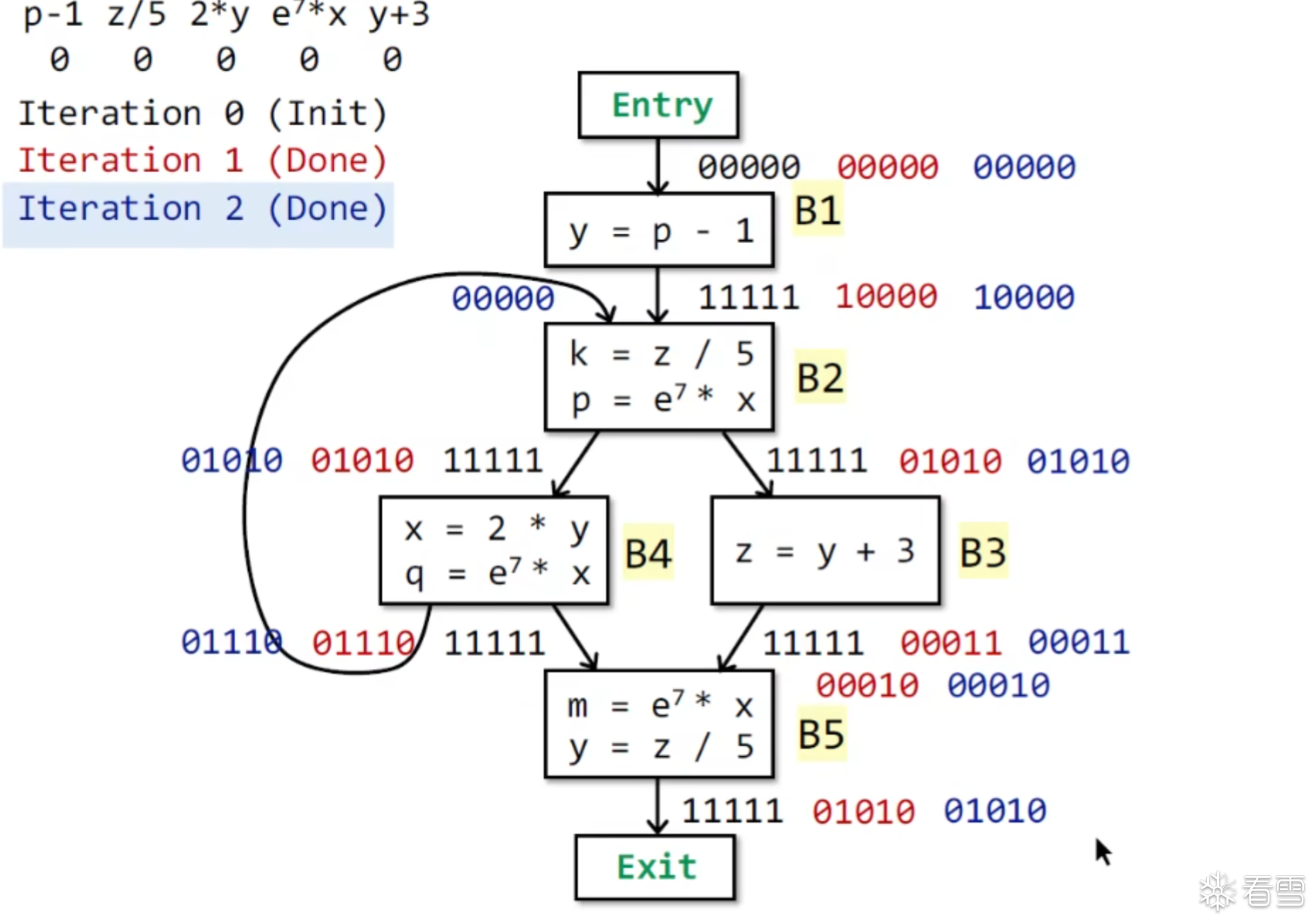
对于给定的CFG图有K个节点这个迭代算法就是在每次循环的时候更新所有节点的OUT[n]
这里我们假设数据流分析中的值的抽象的域为V,我们就能定义一个K Tuple,其中每一个元素的值域为V1到VK 对于这个set的总值域为 V的k次方 记作 Vk
每一次迭代可以看做将一个VK映射到一个新元素的VK通过一个抽象的函数F
这个算法的输出当前仅当K tuple不再变化时即可得到最后的结果.
对于不动点我们有疑问，这个迭代算法
偏序集主要有 偏序关系和一个集合组成的二元组构成
只要该集合和偏序关系满足
我们就称这个偏序关系和这个集合为 偏序集 (Partial Ordering) 简称poset
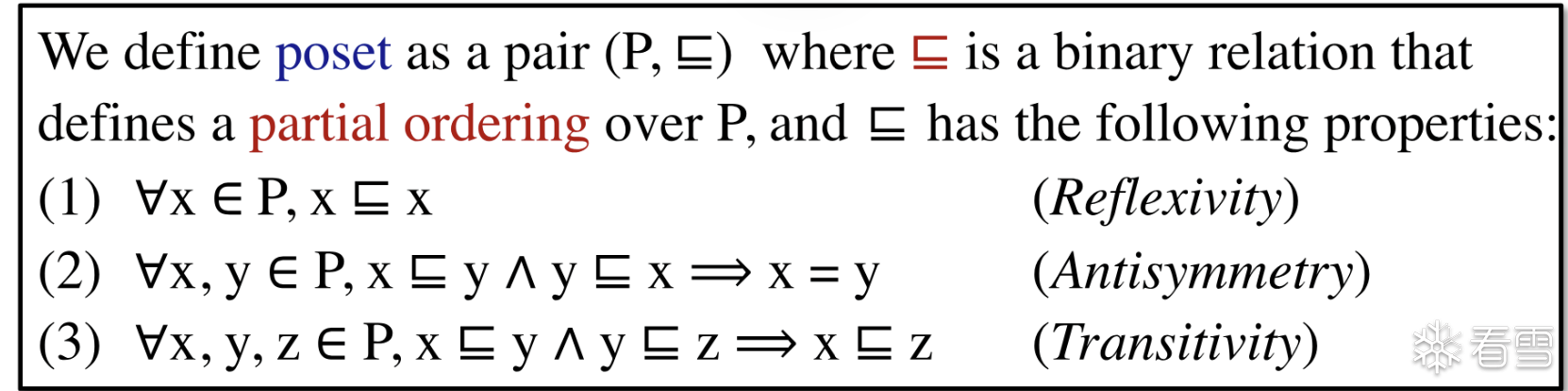
exp1
对于该题我们主要进行判断3个特性
综上所述 对于偏序关系为小于等于的整数集合 是偏序集合
exp2
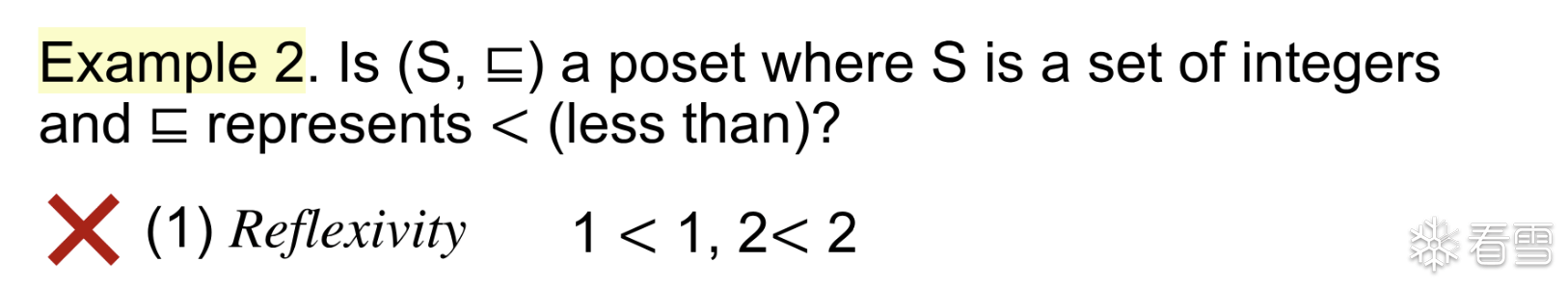
不满足 自反性 不是Poset
exp3
是Poset
exp4
这个题是典型例子需要记住这个 集合结构
在偏序集合中，允许存在不可比较的元素对。如果两个元素 a 和 b 既不满足 a ≤ b 也不满足 b ≤ a，我们就说它们是不可比的（incomparable）。
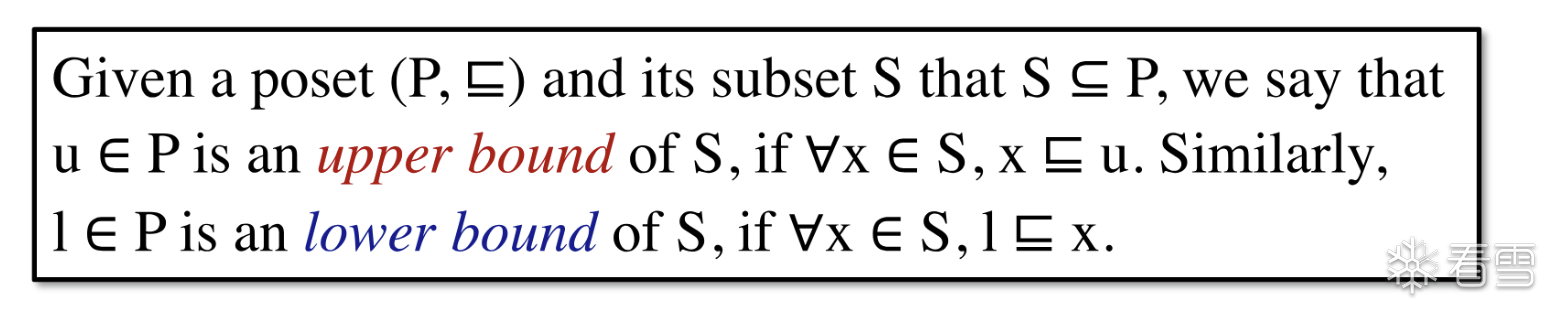
上界
给定一个 poset P 和他的子集S 如果在 P中存在一个元素u满足S中的所有的元素都小于(偏序关系) 这个元素 u则称该元素 u是 集合S的 上界,值得注意的是这里的元素u 必须 对于子集S 全部 compareble.
下界
给定一个 poset P 和他的子集S 如果在 P中存在一个元素l满足S中的所有的元素都大于(偏序关系) 这个元素l则称该元素 l是 集合S的 下界,值得注意的是这里的元素u 必须 对于子集S 全部 compareble.
exp1
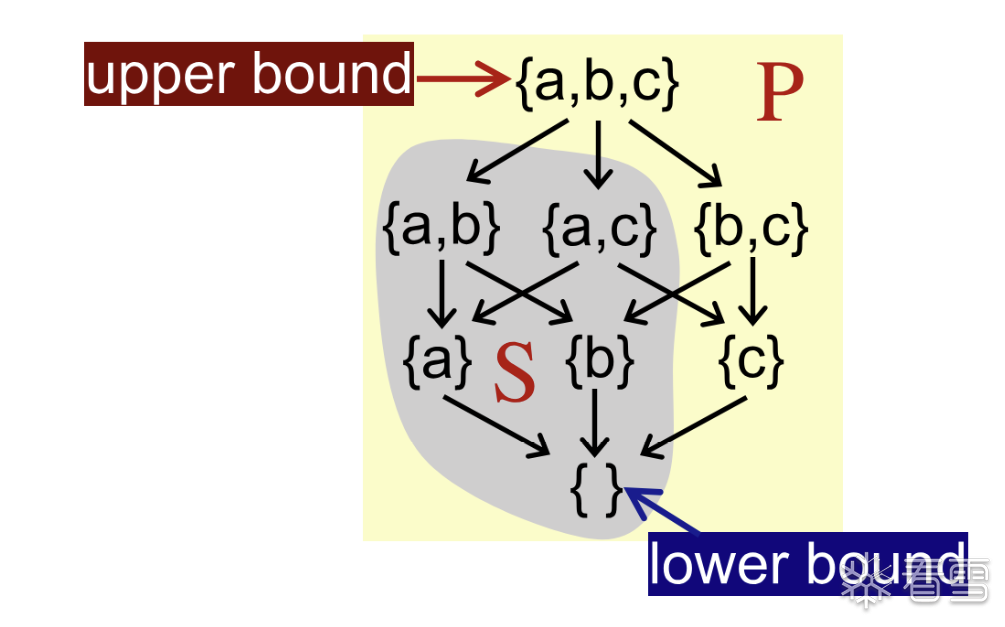
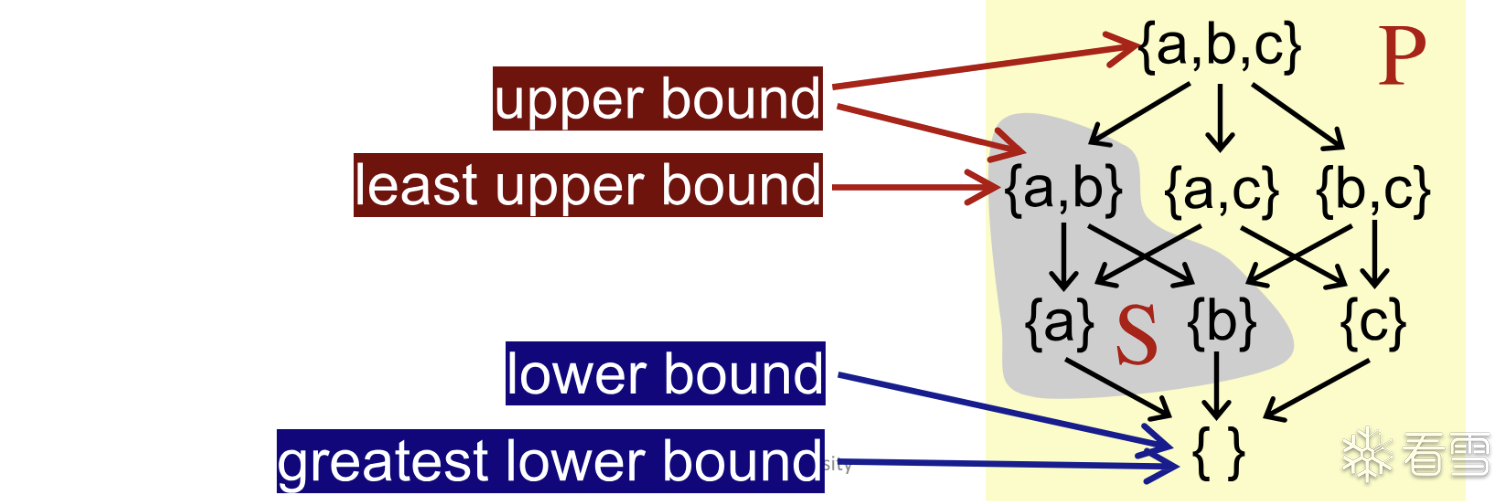
u 是最小的上界：对于 S 的任意上界 v，都有 u ≤ v
l 是最大的下界：对于 S 的任意下界 v，都有 v ≤ l
仅有两个元素的上下界可以如下写
具体证明可以通过自反性证明，glb 或者 lub 是唯一的。
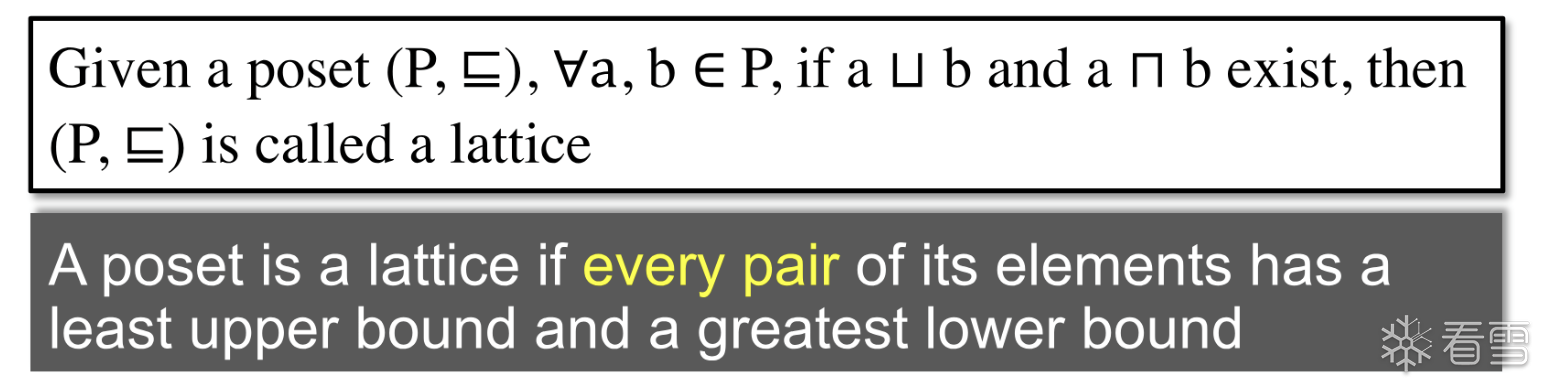
如果一个 poset 中的每一对元素都有 glb 和 lub 则称为格
exp1
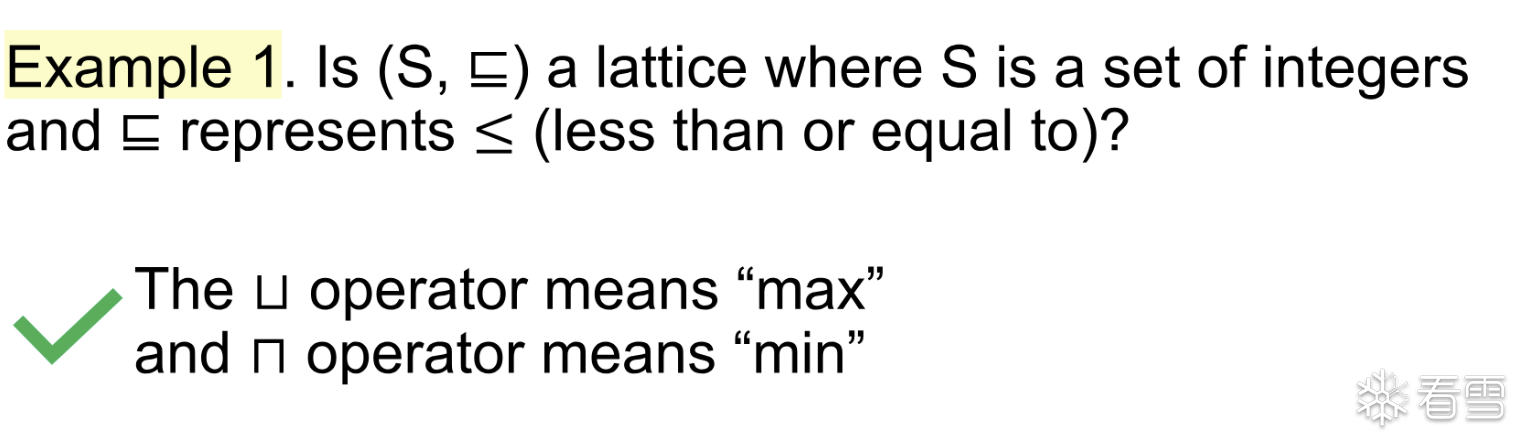
exp2
pin 和 sin 没有lub 所以不是 Lattice
exp3
两两之间都有 glb 和 lub 所以是格
对于一个poset 如果 只有一个glb 或者只有一个lub 则称之为semilattice 半格
|
|
|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
本身涉及到的数学就已经够抽象了，老师如果不认真讲的话很难融汇贯通的 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
